题目内容
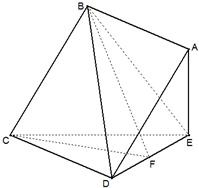 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=3,F为线段DE上的动点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=3,F为线段DE上的动点.(Ⅰ)若F为DE的中点,求证:BE∥平面ACF;
(Ⅱ)若二面角E-BC-F与二面角F-BC-D的大小相等,求DF长.
分析:(I)连接AC,BD交于O,连OF,利用三角形的中位线平行于底边得到OF∥BE,利用直线与平面平行的判定定理得证.
(II)法一:利用二面角的平面角的定义,通过作辅助线,利用线面垂直的判定定理及线面垂直的性质找出二面角E-BC-D的平面角与二面角F-BC-D的平面角,利用已知条件得到线段的长度关系.
法二:通过建立空间直角坐标系,求出两个面的法向量,利用向量的数量积公式求出二面角E-BC-F的余弦值,同理求出二面角D-BC-F的余弦值,根据已知它们的绝对值相等,列出方程求出DF的长度.
(II)法一:利用二面角的平面角的定义,通过作辅助线,利用线面垂直的判定定理及线面垂直的性质找出二面角E-BC-D的平面角与二面角F-BC-D的平面角,利用已知条件得到线段的长度关系.
法二:通过建立空间直角坐标系,求出两个面的法向量,利用向量的数量积公式求出二面角E-BC-F的余弦值,同理求出二面角D-BC-F的余弦值,根据已知它们的绝对值相等,列出方程求出DF的长度.
解答: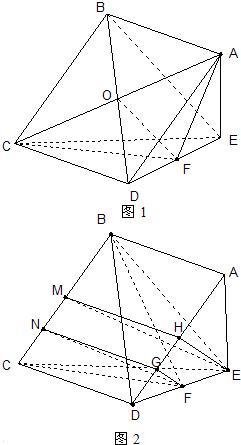 证明:(Ⅰ)连接AC,BD交于O,连OF,如图1
证明:(Ⅰ)连接AC,BD交于O,连OF,如图1
∵F为DE中点,O为BD中点,
∴OF∥BE,OF?平面ACF,BE?平面ACF,
∴BE∥平面ACF.…(6分)
(Ⅱ)如图2,过E作EH⊥AD于H,过H作MH⊥BC
于M,连接ME,同理过F作FG⊥AD于G,过G作NG⊥BC于N,连接NF,
∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,EH?平面DAE,
∴CD⊥EH,CD∩AD=D,CD,AD?平面ABCD,EH⊥平面ABCD,
∴HE⊥BC,
∴BC⊥平面MHE,
∴∠HME为二面角E-BC-D的平面角,
同理,∠GNF为二面角F-BC-D的平面角,
∵MH∥AB,
∴MH=3
,
又HE=
,
∴tan∠HME=
,而∠HME=2∠GNF,
∴tan∠GNF=
-2,
∴
=
-2,GF=3
-6
,
又GF∥HE,
∴
=
,
∴DF=6
-12.…(15分)
解法二:
(Ⅱ)∵AE⊥平面CDE,CD?平面CDE,∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,如图建立坐标系,
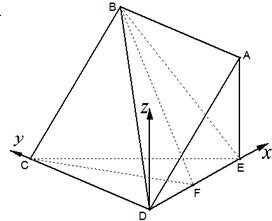 则E(3,0,0),F(a,0,0),C(0,3
则E(3,0,0),F(a,0,0),C(0,3
,0),A(3,0,3),D(0,0,0)
由
=
得B(3,3
,3),设
⊥平面ABCD,
且
=(x,y,z),
由
⇒
⇒
=(1,0,-1)
设
⊥平面BCF,且
=(x,y,z),
由
⇒
⇒
=(3
,a,-3
)
设
⊥平面BCE,且
=(x,y,z),
由
⇒
⇒
=(
,1,-
)
设二面角E-BC-F的大小为α,二面角D-BC-F的大小为β,α=β,|cos<
,
>|=|cos<
,
>|,
∴
=
⇒6=
⇒a=-12±6
,
∵0<a<3,∴a=6
-12.…(15分)
 证明:(Ⅰ)连接AC,BD交于O,连OF,如图1
证明:(Ⅰ)连接AC,BD交于O,连OF,如图1∵F为DE中点,O为BD中点,
∴OF∥BE,OF?平面ACF,BE?平面ACF,
∴BE∥平面ACF.…(6分)
(Ⅱ)如图2,过E作EH⊥AD于H,过H作MH⊥BC
于M,连接ME,同理过F作FG⊥AD于G,过G作NG⊥BC于N,连接NF,
∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,EH?平面DAE,
∴CD⊥EH,CD∩AD=D,CD,AD?平面ABCD,EH⊥平面ABCD,
∴HE⊥BC,
∴BC⊥平面MHE,
∴∠HME为二面角E-BC-D的平面角,
同理,∠GNF为二面角F-BC-D的平面角,
∵MH∥AB,
∴MH=3
| 2 |
又HE=
3
| ||
| 2 |
∴tan∠HME=
| 1 |
| 2 |
∴tan∠GNF=
| 5 |
∴
| GF |
| GN |
| 5 |
| 10 |
| 2 |
又GF∥HE,
∴
| DF |
| DE |
| GF |
| EH |
∴DF=6
| 5 |
解法二:
(Ⅱ)∵AE⊥平面CDE,CD?平面CDE,∴AE⊥CD,
∵CD⊥AD,AE∩AD=A,AD,AE?平面DAE,
∴CD⊥平面DAE,如图建立坐标系,
 则E(3,0,0),F(a,0,0),C(0,3
则E(3,0,0),F(a,0,0),C(0,3| 2 |
由
| DC |
| AB |
| 2 |
| n1 |
且
| n1 |
由
|
|
| n1 |
设
| n2 |
| n2 |
由
|
|
| n2 |
| 2 |
| 2 |
设
| n3 |
| n3 |
由
|
|
| n2 |
| 2 |
| 2 |
设二面角E-BC-F的大小为α,二面角D-BC-F的大小为β,α=β,|cos<
| n1 |
| n2 |
| n3 |
| n2 |
∴
|
| ||||
|
|
|
| ||||
|
|
| |12+a| | ||
|
| 5 |
∵0<a<3,∴a=6
| 5 |
点评:主要考查了空间直线与平面的位置关系和二面角等基础知识,同时考查了空间想象能力、推理论证能力和运算求解能力.
在高考中以解答题的形式出现,常用的工具是空间向量.
在高考中以解答题的形式出现,常用的工具是空间向量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
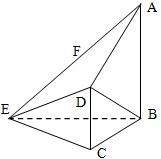 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.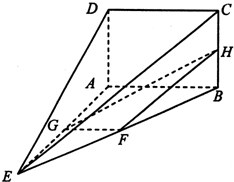 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,