题目内容

如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
(I)求证:平面ADE⊥平面ABE;
(II)求二面角A-EB-D的大小的余弦值.
分析:(Ⅰ) 取BE的中点O,AE的中点F,连OC,OF,DF,则2OF
BA,由AB⊥平面BCE,CD⊥平面BCE,知2CD
BA,由此能够证明平面ADE⊥平面ABE.
(Ⅱ)取BE的中点O,连OC.以O为原点建立如图空间直角坐标系O-xyz,利用向量法能够求出二面角A-EB-D的余弦值.
解答:(Ⅰ) 证明:取BE的中点O,AE的中点F,连OC,OF,DF,则2OF
BA
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD
BA,
∴OF
CD,∴OC∥FD,
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE,从而OC⊥AB.
∴OC⊥平面ABE,∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.…(6分)
(Ⅱ)取BE的中点O,连OC.
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE,∴OF⊥平面BCE.
故可以O为原点建立如图空间直角坐标系O-xyz,
由已知条件有:B(0,
,0),
E(0,-,0),D(1,0,1),
设平面BDE的法向量为
=(x2,y2,z2),
则由
•=
x2+y2+z2=0及
•=2
y
2=0,
取
=(1,0,-1),
∵平面ABE的法向量可取为
=(1,0,0),
∴二面角A-EB-D的余弦值为cos<
,>=
=
,
∴二面角A-EB-D的余弦值为
.…(12分)
点评:本题考查平面与平面垂直的证明,考查二面角的求法.解题时要认真审题,仔细解答,注意等价转化思想和向量法的合理运用.
练习册系列答案
相关题目
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
 阅读快车系列答案
阅读快车系列答案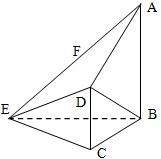 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点. (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,