题目内容
【题目】已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,求分别满足下列条件的a,b的值.
(1)直线l1过点(﹣3,﹣1),且l1⊥l2;
(2)l1∥l2 , 且坐标原点到l1与l2的距离相等.
【答案】解:(1)∵l1⊥l2 ,
∴a(a﹣1)+(﹣b)1=0,即a2﹣a﹣b=0①
又点(﹣3,﹣1)在l1上,
∴﹣3a+b+4=0②
由①②得a=2,b=2.
(2)∵l1∥l2 , ∴![]() =1﹣a,∴b=
=1﹣a,∴b=![]() ,
,
故l1和l2的方程可分别表示为:
(a﹣1)x+y+![]() =0,(a﹣1)x+y+
=0,(a﹣1)x+y+![]() =0,
=0,
又原点到l1与l2的距离相等.
∴4|![]() |=|
|=|![]() |,∴a=2或a=
|,∴a=2或a=![]() ,
,
∴a=2,b=﹣2或a=![]() ,b=2.
,b=2.
【解析】(1)利用直线l1过点(﹣3,﹣1),直线l1与l2垂直,斜率之积为﹣1,得到两个关系式,求出a,b的值.
(2)类似(1)直线l1与直线l2平行,斜率相等,坐标原点到l1 , l2的距离相等,利用点到直线的距离相等.得到关系,求出a,b的值.
【考点精析】根据题目的已知条件,利用点到直线的距离公式的相关知识可以得到问题的答案,需要掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: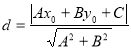 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目