题目内容
已知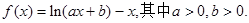
(1)求使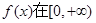 上是减函数的充要条件;
上是减函数的充要条件;
(2)求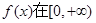 上的最大值。
上的最大值。
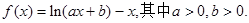
(1)求使
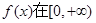 上是减函数的充要条件;
上是减函数的充要条件;(2)求
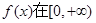 上的最大值。
上的最大值。(1)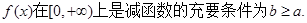
(2)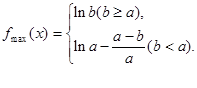
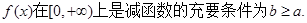
(2)
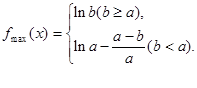
试题分析:(1)
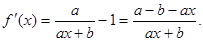
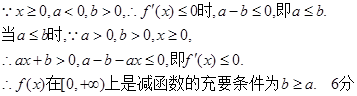
(2)由(1)知,当
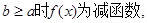

最大值为
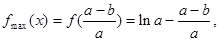
即
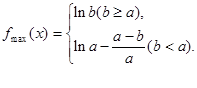 12分
12分点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。通过比较极值、区间端点函数值的大小,得到函数的最值。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目
题目内容
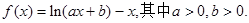
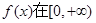 上是减函数的充要条件;
上是减函数的充要条件;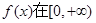 上的最大值。
上的最大值。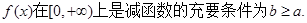
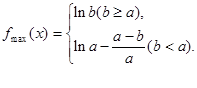
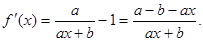
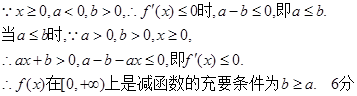
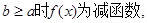

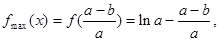
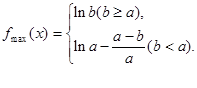 12分
12分