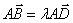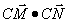题目内容
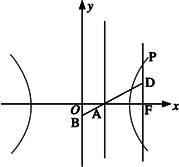
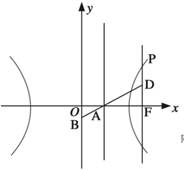
如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且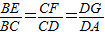 ,P为GE与OF的交点,建立如图坐标系,求P点的轨迹方程.
,P为GE与OF的交点,建立如图坐标系,求P点的轨迹方程.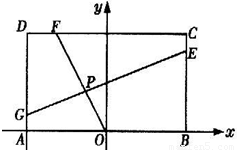
【答案】分析:根据如图坐标系,按题意写出A,B,C,D四点的坐标,进而根据 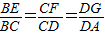 解出E,F,G三点的坐标 参数表示,求出OF与GE两条直线的方程,两者联立即可求出点P的坐标满足的参数方程,消去参数,得到点P的轨迹方程.
解出E,F,G三点的坐标 参数表示,求出OF与GE两条直线的方程,两者联立即可求出点P的坐标满足的参数方程,消去参数,得到点P的轨迹方程.
解答:解:如图,按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a).
设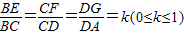 .
.
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:2ax+(2k-1)y=0,①
直线GE的方程为:-a(2k-1)x+y-2a=0②
从①,②消去参数k,
得点P(x,y)坐标满足方程2a2x2+y2-2ay=0,(矩形内部).
点评:考查解析法求点的轨迹方程,本题在做题时引入了参数k,故得到的轨迹方程为参数方程,需要消去参数得到轨迹方程,又当字母的取值范围对曲线的形状有影响时,要对其范围进行讨论以确定轨迹的具体性状.
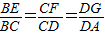 解出E,F,G三点的坐标 参数表示,求出OF与GE两条直线的方程,两者联立即可求出点P的坐标满足的参数方程,消去参数,得到点P的轨迹方程.
解出E,F,G三点的坐标 参数表示,求出OF与GE两条直线的方程,两者联立即可求出点P的坐标满足的参数方程,消去参数,得到点P的轨迹方程.解答:解:如图,按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a).
设
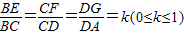 .
.由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:2ax+(2k-1)y=0,①
直线GE的方程为:-a(2k-1)x+y-2a=0②
从①,②消去参数k,
得点P(x,y)坐标满足方程2a2x2+y2-2ay=0,(矩形内部).
点评:考查解析法求点的轨迹方程,本题在做题时引入了参数k,故得到的轨迹方程为参数方程,需要消去参数得到轨迹方程,又当字母的取值范围对曲线的形状有影响时,要对其范围进行讨论以确定轨迹的具体性状.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
如图,已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且