题目内容
14.已知矩阵$M=({\begin{array}{l}1&a\\ 0&b\end{array}})$,其中a,b∈R.若点P(1,-2)在矩阵M的变换下得到点P′(-1,-4).(Ⅰ)求实数a,b的值;
(Ⅱ)若$\overrightarrow a=({\begin{array}{l}2\\ 1\end{array}})$,求M10$\overrightarrow a$.
分析 (Ⅰ)通过$({\begin{array}{l}1&a\\ 0&b\end{array}})$$({\begin{array}{l}1\\{-2}\end{array}})$=$({\begin{array}{l}{-1}\\{-4}\end{array}})$计算即可;
(Ⅱ)令特征多项式$f(λ)=|{\begin{array}{l}{λ-1}&{-1}\\ 0&{λ-2}\end{array}}|$=0,可得特征值λ1=1,λ2=2,进而可得对应的特征向量,计算即得结论.
解答 解:(Ⅰ)由$({\begin{array}{l}1&a\\ 0&b\end{array}})$$({\begin{array}{l}1\\{-2}\end{array}})$=$({\begin{array}{l}{-1}\\{-4}\end{array}})$,得$\left\{{\begin{array}{l}{1-2a=-1}\\{-2b=-4}\end{array}}\right.$,
∴$\left\{{\begin{array}{l}{a=1}\\{b=2}\end{array}}\right.$;
(Ⅱ)由(I)知$M=({\begin{array}{l}1&1\\ 0&2\end{array}})$.
令$f(λ)=|{\begin{array}{l}{λ-1}&{-1}\\ 0&{λ-2}\end{array}}|$=(λ-1)(λ-2)=0,
解得λ1=1,λ2=2.
属于λ1=1的一个特征向量$\overrightarrow{e_1}=({\begin{array}{l}1\\ 0\end{array}})$,
属于λ2=2的一个特征向量$\overrightarrow{e_2}=({\begin{array}{l}1\\ 1\end{array}})$,
∴$\overrightarrow a=\overrightarrow{e_1}+\overrightarrow{e_2}$.
∴${M^{10}}\overrightarrow a={M^{10}}({\overrightarrow{e_1}+\overrightarrow{e_2}})$
=${λ_1}^{10}\overrightarrow{e_1}+{λ_2}^{10}\overrightarrow{e_2}$
=$({\begin{array}{l}1\\ 0\end{array}})+{2^{10}}({\begin{array}{l}1\\ 1\end{array}})=({\begin{array}{l}{1025}\\{1024}\end{array}})$.
点评 本题考查矩阵变换,注意解题方法的积累,属于中档题.

| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
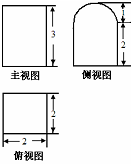
| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
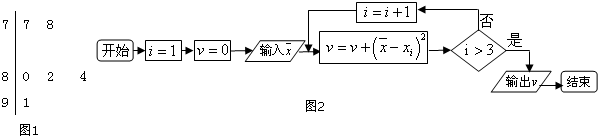 .
.