Question

【题目】对于定义在区间D上的函数f(x)，若存在闭区间[a，b]D和常数c，使得对任意x1∈[a，b]，都有f(x1)＝c，且对任意x2∈D，当x2[a，b]时，f(x2)＜c恒成立，则称函数f(x)为区间D上的“平顶型”函数．给出下列结论：

①“平顶型”函数在定义域内有最大值；

②函数f(x)＝x－|x－2|为R上的“平顶型”函数；

③函数f(x)＝sin x－|sin x|为R上的“平顶型”函数；

④当t≤时，函数f(x)＝是区间[0，＋∞)上的“平顶型”函数．

其中正确的结论是________．(填序号)

Answer 1

【答案】①②④

【解析】

由于“平顶型”函数在区间D上对任意x1∈[a，b]，都有f(x1)＝c，且对任意x2∈D，当x2[a，b]时，f(x2)＜c恒成立，所以“平顶型”函数在定义域内有最大值c，①正确；对于函数f(x)＝x－|x－2|，当x≥2时，f(x)＝2，当x＜2时，f(x)＝2x－2＜2，所以②正确；函数f(x)＝sin x－|sin x|是周期为2π的函数，所以③不正确；对于函数f(x)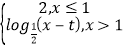＝，当x≤1时，f(x)＝2，当x＞1时，f(x)＜2，所以④正确．

答案：①②④