题目内容
【题目】若正数x,y满足x+3y=5xy,求:
(1)3x+4y的最小值;
(2)求xy的最小值.
【答案】解:(1)∵正数x,y满足x+3y=5xy,∴y=![]() >0,解得
>0,解得![]() .
.
∴3x+4y=3x+![]() =f(x),
=f(x),
f′(x)=3+![]() =
=![]() ,
,
∴当x>1时,f′(x)>0,此时函数f(x)单调递增;当1>x>![]() 时,f′(x)<0,此时函数f(x)单调递减.
时,f′(x)<0,此时函数f(x)单调递减.
∴当x=1时,f(x)取得最小值,f(1)=3+2=5.
∴3x+4y的最小值为1.
(2)∵正数x,y满足x+3y=5xy,
∴5xy≥2![]() ,
,
解得:xy≥![]() ,当且仅当x=3y=
,当且仅当x=3y=![]() 时取等号.
时取等号.
∴xy的最小值为![]() .
.
【解析】(1)法一:由正数x,y满足x+3y=5xy,可得y=![]() >0,解得
>0,解得![]() .3x+4y=3x+
.3x+4y=3x+![]() =f(x),利用导数研究函数的单调性极值与最值即可得出.
=f(x),利用导数研究函数的单调性极值与最值即可得出.
(2)正数x,y满足x+3y=5xy,利用基本不等式的性质即可得出.
【考点精析】通过灵活运用基本不等式,掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
相关题目
【题目】光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
第t天 | 10 | 17 | 21 | 30 |
Q(件) | 180 | 152 | 136 | 100 |
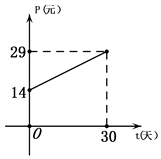
(1)根据图象写出销售价格与时间t的函数关系式P=f(t).
(2)请根据表中数据写出日销售量Q与时间t的函数关系式Q=g(t).
(3)设日销售额为M(单位:元),请求出这30天中第几日M最大,最大值为多少?