题目内容
11.设a>0,b>0,2c>a+b,求证:(1)c2>ab;
(2)c-$\sqrt{{c}^{2}-ab}$<a<c+$\sqrt{{c}^{2}-ab}$.
分析 (1)根据基本不等式的证明即可证明c2>ab;
(2)利用分析法进行证明.
解答 证明:(1)∵a>0,b>0,2c>a+b$≥2\sqrt{ab}$,
∴c>$\sqrt{ab}$,
平方得c2>ab;
(2)要证c-$\sqrt{{c}^{2}-ab}$<a<c+$\sqrt{{c}^{2}-ab}$.
只要证-$\sqrt{{c}^{2}-ab}$<a-c<$\sqrt{{c}^{2}-ab}$.
即证|a-c|<$\sqrt{{c}^{2}-ab}$,
即(a-c)2<c2-ab,
∵(a-c)2-c2+ab=a(a+b-2c)<0成立,
∴原不等式成立.
点评 本题主要考查不等式的证明,利用不等式的性质结合分析法是解决本题的关键.

练习册系列答案
相关题目
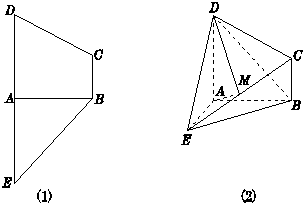 如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.
如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.