题目内容
在数列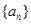 中,
中,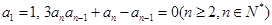 .
.
(1)求数列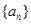 的通项;
的通项;
(2)若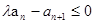 对任意的正整数
对任意的正整数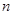 恒成立,求实数
恒成立,求实数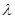 的取值范围.
的取值范围.
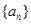 中,
中,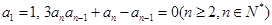 .
.(1)求数列
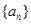 的通项;
的通项;(2)若
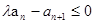 对任意的正整数
对任意的正整数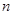 恒成立,求实数
恒成立,求实数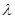 的取值范围.
的取值范围.(1)an= ;(2)λ∈(﹣∞,
;(2)λ∈(﹣∞, ].
].
 ;(2)λ∈(﹣∞,
;(2)λ∈(﹣∞, ].
].试题分析:(1)将3anan﹣1+an﹣an﹣1=0(n≥2)整理得:
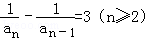 ,可得{
,可得{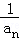 }为等差数列,由此求出数列{
}为等差数列,由此求出数列{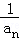 }的通项公式,即可求得数列{an}的通项公式;
}的通项公式,即可求得数列{an}的通项公式;(2)把(1)求得的结果代入λan﹣an+1≤0,分离参数,得到λ≤
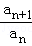 ,转化为求函数的最小值即可解决;
,转化为求函数的最小值即可解决;试题分析:(1)由题意知数列各项不为0,
由3anan﹣1+an﹣an﹣1=0,得3+
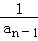 ﹣
﹣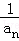 =0,
=0,所以
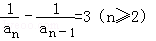 ,
,所以数列{
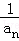 }为等差数列,首项为1,公差为3,
}为等差数列,首项为1,公差为3,则
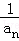 =1+(n﹣1)•3=3n﹣2,所以an=
=1+(n﹣1)•3=3n﹣2,所以an= ;
;(2)若λan﹣an+1≤0恒成立,即λ≤
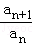 恒成立,整理得:λ≤
恒成立,整理得:λ≤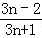 =1﹣
=1﹣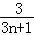 ,
,设f(x)=1﹣
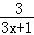 ,可知f(x)在x∈(﹣
,可知f(x)在x∈(﹣ ,+∞)上单调递增,
,+∞)上单调递增,所以当n=1时,[1﹣
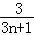 ]min=
]min= ,
,所以λ的取值范围为λ∈(﹣∞,
 ].
].
练习册系列答案
相关题目
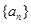 中,
中,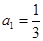 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的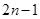 倍(
倍(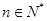 ).
). 的前n项和为
的前n项和为 ,若
,若 =-2,
=-2, =3,则m=( )
=3,则m=( ) 满足:
满足: (m为正整数),
(m为正整数), 若
若 ,则m所有可能的取值为________。
,则m所有可能的取值为________。 中,
中, ,则
,则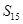 = .
= . 与
与 的前
的前 项和分别是
项和分别是 和
和 ,已知
,已知 ,则
,则 等于( )
等于( )


 满足
满足 ,则
,则 ________.
________.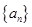 的前
的前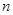 项和为
项和为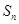 ,且
,且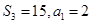 ,则
,则 ______.
______.