题目内容
(本小题满分12分)
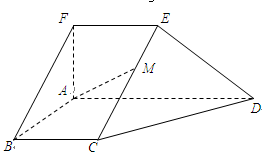
如图,直三棱柱ABC—A1B1C1中,AC=BC=1,∠ACB=90°,AA1= ,D是A1B1中点.
,D是A1B1中点.
(1)求证:C1D⊥AB1 ;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.
(1)C1D⊥平面AA1B1B.(2)点F为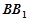 的中点.
的中点.
解析试题分析:(1)证明:如图,
∵ ABC—A1B1C1是直三棱柱,
∴ A1C1=B1C1=1,且∠A1C1B1=90°.
又 D是A1B1的中点,∴ C1D⊥A1B1.-------------3分
∵ AA1⊥平面A1B1C1,C1D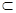 平面A1B1C1,
平面A1B1C1,
∴ AA1⊥C1D,∴ C1D⊥平面AA1B1B.
∴C1D⊥AB1-----------------------------------6分
(2)解:作DF⊥AB1交AB1于E,DF交BB1于F,连结C1F,
又由(1)C1D⊥AB1
则AB1⊥平面C1DF,点F即为所求.---------------------9分
连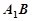 ∵
∵ 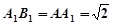 即四边形
即四边形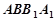 为正方形.
为正方形.
∴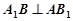
∴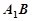 ∥
∥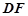 又D是A1B1的中点,点F为
又D是A1B1的中点,点F为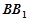 的中点.------------12分
的中点.------------12分
考点:线面垂直的判定定理;线面垂直的性质定理;直棱柱的结构特征。
点评:①本题主要考查了空间的线线垂直的证明,充分考查了学生的逻辑推理能力,空间想象力,以及识图能力。②我们要熟练掌握正棱柱、直棱柱的结构特征。正棱柱:底面是正多边形,侧棱垂直底面。直棱柱:侧棱垂直底面。

练习册系列答案
相关题目
 所在平面与平面
所在平面与平面 垂直,
垂直, ,且
,且 ,
, 为
为 上的动点.
上的动点.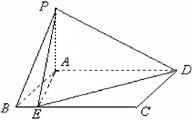
 ;
; ,在线段
,在线段 的大小为
的大小为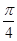 . 若存在,确定点E的位置,若不存在,说明理由.
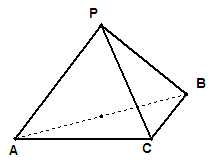
. 若存在,确定点E的位置,若不存在,说明理由.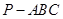 中,
中,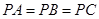 ,
,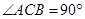 ,
,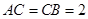 .
. 
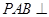 平面
平面 ;
;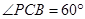 时,求三棱锥
时,求三棱锥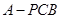 的体积.
的体积. ,
,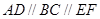 ,
,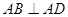 ,
,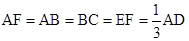
 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由. 的菱形
的菱形 中,
中, ,
, 面
面 ,
, 、
、 分别是
分别是 和
和 的中点.
的中点.
 面
面 ;
;  ⊥平面
⊥平面 ;
; 与平面
与平面 中,底面
中,底面 是直角梯形,
是直角梯形, ∥
∥ ,∠
,∠ ,
,  ,平面
,平面 ⊥平面
⊥平面 .
.
 和平面
和平面 所成二面角(小于
所成二面角(小于 )的大小;
)的大小; 上是否存在点
上是否存在点 使得
使得 ∥平面
∥平面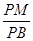 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  为圆
为圆 的直径,点
的直径,点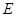 、
、 在圆
在圆 ,矩形
,矩形 所在的平面与圆
所在的平面与圆 ,
, .
.
 平面
平面 ;
;  的长为何值时,平面
的长为何值时,平面 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为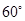 ?
? 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.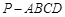 中,
中,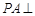 平面
平面 ,
,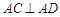 ,
,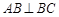 ,
,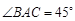 ,
,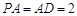 ,
,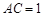 .
.
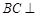 平面
平面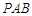
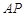 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;