题目内容
(本小题满分13分) 已知命题p:x∈A={x|a-1<x<a+1,x∈R},命题
q:x∈B={x|x2-4x+3≥0}.
(1)或A∩B=∅,A∪B=R,求实数a
(2)若 是p的必要条件,求实数a.
是p的必要条件,求实数a.
【答案】
(1) a=2;(2) a=2
【解析】本试题主要考查了命题的真值,以及集合的运算的综合运用,以及二次不等式的求解问题。
(1)由题意得B={x|x≥3或x≤1},-------2分
由A∩B=∅,A∪B=R,可知A=∁RB=(1,3)从而得到结论。
(2)∵B={x|x≥3或x≤1},∴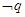 :x∈{x|1<x<3}.--------8分
:x∈{x|1<x<3}.--------8分
∵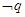 是p的必要条件.即p⇒
是p的必要条件.即p⇒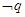 ,
,
那么可以得到集合间的关系,A⊆∁RB=(1,3),从而得到参数a的范围。
解:(1)由题意得B={x|x≥3或x≤1},-------2分
由A∩B=∅,A∪B=R,可知A=∁RB=(1,3)--------4分
∴ ⇒a=2---------6分
⇒a=2---------6分
(2)∵B={x|x≥3或x≤1},∴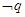 :x∈{x|1<x<3}.--------8分
:x∈{x|1<x<3}.--------8分
∵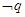 是p的必要条件.即p⇒
是p的必要条件.即p⇒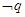 ,
,
∴A⊆∁RB=(1,3)-------10分
∴ ⇒2≤a≤2⇒a=2.--------13分
⇒2≤a≤2⇒a=2.--------13分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和