题目内容
如图,△ABC中,D,E分别是BC,AC的中点,设AD与BE相交于G,求证:AG:GD=BG:GE=2:1.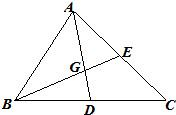
分析:根据两个点分别是三角形两条边的中点,得到这条线是三角形的中位线,两条线之间是平行关系,得到两个三角形相似,对应边成比例,又根据中位线得到比值.
解答:证明:连接DE,
∵D,E分别是BC,AC的中点,
∴DE∥AB,DE=
AB
∴△DEG∽△ABG,
∴AG:GD=BG:GE=AB:DE=2:1
∵D,E分别是BC,AC的中点,
∴DE∥AB,DE=
| 1 |
| 2 |
∴△DEG∽△ABG,
∴AG:GD=BG:GE=AB:DE=2:1
点评:本题考查三角形的中位线定理,考查三角形相似的判定,考查相似三角形的对应边成比例,本题是一个基础题,考查的知识点比较简单.

练习册系列答案
相关题目
 如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,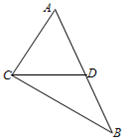 如图,△ABC中,D为边AB上的点,∠CAD=60°,CD=21,CB=31,DB=20.
如图,△ABC中,D为边AB上的点,∠CAD=60°,CD=21,CB=31,DB=20.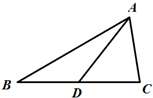 如图,△ABC中,D是BC边上的中线,且
如图,△ABC中,D是BC边上的中线,且 (2012•珠海一模)(几何证明选讲选做题)
(2012•珠海一模)(几何证明选讲选做题)