题目内容
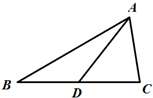如图，△ABC中，D是BC边上的中线，且BC=2| 2 |
| 3 |
2
+2
| 2 |
| 5 |
2
+2
．| 2 |
| 5 |
分析：根据平面向量加减法的运算法则与向量数量积的运算性质，算出2（
2+
2）=4|
|2+|
|2=20．再利用基本不等式，证出（
+
）2≤2（
2+
2）=20，从而得出当
=
时，
+
的最大值为2
，由此即可得到△ABC周长的最大值．
| |AB| |
| |AC| |
| AD |
| BC |
| |AB| |
| |AC| |
| |AB| |
| |AC| |
| |AB| |
| |AC| |
| |AB| |
| |AC| |
| 5 |
解答：解：∵△ABC中，D是BC边上的中线，
∴
+
=2
，两边平方得（
+
）2=4
2=4|
|2=12．…①
又∵
=
-
，BC=2
，
∴（
-
）2=
2=|
|2=8．…②
将①②两式相加，可得（
+
）2+（
-
）2=20，
即2（
2+
2）=20，可得
2+
2=10，
由基本不等式，得（
+
）2≤2（
2+
2）=20，
∴
+
≤
=2
，
当且仅当
=
=
时，
+
的最大值为2
，
因此，△ABC周长
+
+
的最大值为2
+2
故答案为：2
+2
．
∴
| AB |
| AC |
| AD |
| AB |
| AC |
| AD |
| AD |
又∵
| BC |
| AC |
| AB |
| 2 |
∴（
| AC |
| AB |
| BC |
| BC |
将①②两式相加，可得（
| AB |
| AC |
| AC |
| AB |
即2（
| AB |
| AC |
| |AB| |
| |AC| |
由基本不等式，得（
| |AB| |
| |AC| |
| |AB| |
| |AC| |
∴
| |AB| |
| |AC| |
| 20 |
| 5 |
当且仅当
| |AB| |
| |AC| |
| 5 |
| |AB| |
| |AC| |
| 5 |
因此，△ABC周长
| |AB| |
| |AC| |
| |BC| |
| 2 |
| 5 |
故答案为：2
| 2 |
| 5 |
点评：本题结合三角形一边长和这条边上的中线长，求三角形周长的最大值，着重考查了利用基本不等式求最值、向量的线性运算法则和向量数量积的运算性质等知识，属于中档题．
练习册系列答案
相关题目
如图，△ABC中，D，E，F分别是边BC，AB，CA的中点，在以A、B、C、D、E、F为端点的有向线段中所表示的向量中，
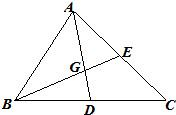
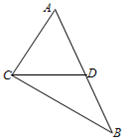如图，△ABC中，D为边AB上的点，∠CAD=60°，CD=21，CB=31，DB=20．
（2012•珠海一模）（几何证明选讲选做题）