题目内容
（2012•珠海一模）（几何证明选讲选做题）如图，△ABC中，D、E分别在边AB、AC上，CD平分∠ACB，DE∥BC，如果AC=10，BC=15，那么AE=
4
4
．分析：首先利用角平分线的性质和两直线平行，内错角相等的性质求证出△EDC是等腰三角形，然后再根据相似三角形对应边的比相等求解．
解答：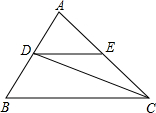
解：∵CD平分∠ACB，
∴∠ECD=∠DCB，
又∵DE∥BC，
∴∠EDC=∠DCB，
∴∠EDC=∠ECD，
∴△EDC是等腰三角形．设AE=x，
则ED=EC=AC-AE=10-x．
∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，即
=
，
∴x=4．
故答案为：4．
解：∵CD平分∠ACB，∴∠ECD=∠DCB，
又∵DE∥BC，
∴∠EDC=∠DCB，
∴∠EDC=∠ECD，
∴△EDC是等腰三角形．设AE=x，
则ED=EC=AC-AE=10-x．
∵DE∥BC，
∴△ADE∽△ABC，
∴
| DE |
| BC |
| AE |
| AC |
| 10-x |
| 15 |
| x |
| 10 |
∴x=4．
故答案为：4．
点评：本题考查的是平行线的性质以及角平分线的性质．本题关键是找出内错角，求出△DEC为等腰三角形，从而求解．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
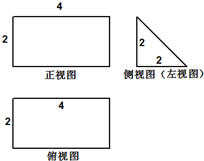（2012•珠海一模）如图，某几何体的正视图和俯视图都是矩形，侧视图是等腰直角三角形，则该几何体的体积为（ ）
（2012•珠海一模）如图，在△ABC中，已知