题目内容
设抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线与抛物线交于A、B两点.(1)若p=2,求线段AF中点M的轨迹方程;
(2)若直线AB的方向向量为
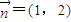 ,当焦点为
,当焦点为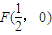 时,求△OAB的面积;
时,求△OAB的面积;(3)若M是抛物线C准线上的点,求证:直线MA、MF、MB的斜率成等差数列.
【答案】分析:(1)先由抛物线的方程得到其焦点坐标,设A(x,y),M(x,y),利用中点坐标公式得 ,最后根据抛物线方程消去参数x,y,即得线段AF中点M的轨迹方程.
,最后根据抛物线方程消去参数x,y,即得线段AF中点M的轨迹方程.
(2)先利用直线AB的方向向量,求出直线的斜率,得出直线方程;再与抛物线方程联立,求出A、B两点之间的线段长以及点O到AB的距离,代入△ABO面积的表达式,求出△ABO面积即可.
(3)显然直线MA、MB、MF的斜率都存在,分别设为k1、k2、k3.直线AB的方程与抛物线方程联立,结合根与系数的关系,证出k1+k2=2k3即可证得kMA、kMF、kMB成等差数列.
解答:解:(1)设A(x,y),M(x,y),焦点F(1,0),
则由题意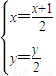 ,即
,即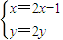 …2分
…2分
所求的轨迹方程为4y2=4(2x-1),即y2=2x-1…4分
(2)y2=2x, ,直线
,直线 ,…5分
,…5分
由 得,y2-y-1=0,
得,y2-y-1=0,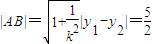 …7分
…7分
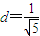 ,…8分
,…8分
 …9分
…9分
(3)显然直线MA、MB、MF的斜率都存在,分别设为k1、k2、k3.
点A、B、M的坐标为 .
.
设直线AB: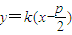 ,代入抛物线得
,代入抛物线得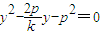 ,…11分
,…11分
所以 ,…12分
,…12分
又 ,
,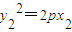 ,
,
因而 ,
,
因而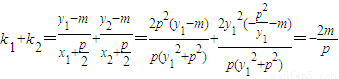 …14分
…14分
而2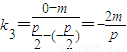 ,故k1+k2=2k3.…16分.
,故k1+k2=2k3.…16分.
点评:本小题主要考查轨迹方程、圆锥曲线的轨迹问题等基础知识,考查运算求解能力,考查数形结合思想、方程思想.属于中档题.
 ,最后根据抛物线方程消去参数x,y,即得线段AF中点M的轨迹方程.
,最后根据抛物线方程消去参数x,y,即得线段AF中点M的轨迹方程.(2)先利用直线AB的方向向量,求出直线的斜率,得出直线方程;再与抛物线方程联立,求出A、B两点之间的线段长以及点O到AB的距离,代入△ABO面积的表达式,求出△ABO面积即可.
(3)显然直线MA、MB、MF的斜率都存在,分别设为k1、k2、k3.直线AB的方程与抛物线方程联立,结合根与系数的关系,证出k1+k2=2k3即可证得kMA、kMF、kMB成等差数列.
解答:解:(1)设A(x,y),M(x,y),焦点F(1,0),
则由题意
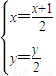 ,即
,即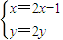 …2分
…2分所求的轨迹方程为4y2=4(2x-1),即y2=2x-1…4分
(2)y2=2x,
 ,直线
,直线 ,…5分
,…5分由
 得,y2-y-1=0,
得,y2-y-1=0,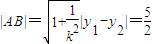 …7分
…7分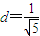 ,…8分
,…8分 …9分
…9分(3)显然直线MA、MB、MF的斜率都存在,分别设为k1、k2、k3.
点A、B、M的坐标为
 .
.设直线AB:
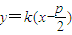 ,代入抛物线得
,代入抛物线得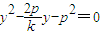 ,…11分
,…11分所以
 ,…12分
,…12分又
 ,
,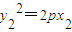 ,
,因而
 ,
,
因而
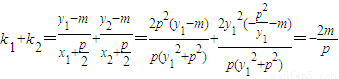 …14分
…14分而2
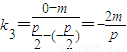 ,故k1+k2=2k3.…16分.
,故k1+k2=2k3.…16分.点评:本小题主要考查轨迹方程、圆锥曲线的轨迹问题等基础知识,考查运算求解能力,考查数形结合思想、方程思想.属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目