题目内容

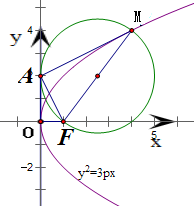
设抛物线C：y2=3px（p＞0）的焦点为F，点M在C上，|MF|=5，若以MF为直径的圆过点（0，2），则C的方程为（　　）
分析：根据抛物线方程算出|OF|=
3p
4
，设以MF为直径的圆过点A（0，2），在Rt△AOF中利用勾股定理算出|AF|=
4+
9p2
16
．再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF，Rt△AMF中利用∠AMF的正弦建立关系式，从而得到关于p的方程，解之得到实数p的值，进而得到抛物线C的方程．
解答：解：∵抛物线C方程为y2=3px（p＞0）
∴焦点F坐标为（
3p
4
，0），可得|OF|=
3p
4

∵以MF为直径的圆过点（0，2），
∴设A（0，2），可得AF⊥AM
Rt△AOF中，|AF|=
22+(
3p
4
)2
=
4+
9p2
16

∴sin∠OAF=
|OF|
|AF|
=
3p
4
4+
9p2
16

∵根据抛物线的定义，得直线AO切以MF为直径的圆于A点，
∴∠OAF=∠AMF，可得Rt△AMF中，sin∠AMF=
|AF|
|MF|
=
3p
4
4+
9p2
16
，
∵|MF|=5，|AF|=
4+
9p2
16

∴
4+
9p2
16
5
=
3p
4
4+
9p2
16
，整理得4+
9p2
16
=
15p
4
，解之可得p=
4
3
或p=
16
3

因此，抛物线C的方程为y2=4x或y2=16x
故选：C
点评：本题给出抛物线一条长度为5的焦半径MF，以MF为直径的圆交抛物线于点（0，2），求抛物线的方程，着重考查了抛物线的定义与简单几何性质、圆的性质和解直角三角形等知识，属于中档题．
练习册系列答案
相关题目
设抛物线C：y2=4x的焦点为F，直线l过F且与C交于A，B两点．若|AF|=3|BF|，则l的方程为（　　）
（2012•长宁区二模）设抛物线C：y2=2px（p＞0）的焦点为F，过F且垂直于x轴的直线与抛物线交于P1，P2两点，已知|P1P2|=8．
（1）求抛物线C的方程；
（2）设m＞0，过点M（m，0）作方向向量为
d
=(1，
3
)的直线与抛物线C相交于A，B两点，求使∠AFB为钝角时实数m的取值范围；
（3）①对给定的定点M（3，0），过M作直线与抛物线C相交于A，B两点，问是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切？若存在，请求出这条直线；若不存在，请说明理由．
②对M（m，0）（m＞0），过M作直线与抛物线C相交于A，B两点，问是否存在一条垂直于x轴的直线与以线段AB为直径的圆始终相切？（只要求写出结论，不需用证明）
（2013•黄浦区二模）设抛物线C：y2=2px（p＞0）的焦点为F，经过点F的动直线l交抛物线C于A（x1，y1），B（x2，y2）两点，且y1y2=-4．
（1）求抛物线C的方程；
（2）若直线2x+3y=0平分线段AB，求直线l的倾斜角．
（3）若点M是抛物线C的准线上的一点，直线MF，MA，MB的斜率分别为k0，k1，k2．求证：当k0=1时，k1+k2为定值．
（2013•黄浦区二模）设抛物线C：y2=2px（p＞0）的焦点为F，经过点F的动直线l交抛物线C于点A（x1，y1），B（x2，y2）且y1y2=-4．
（1）求抛物线C的方程；
（2）若
OE
=2(
OA
+
OB
)（O为坐标原点），且点E在抛物线C上，求直线l倾斜角；
（3）若点M是抛物线C的准线上的一点，直线MF，MA，MB的斜率分别为k0，k1，k2．求证：当k0为定值时，k1+k2也为定值．
设抛物线C：y2=4x的焦点为F，直线l过F且与C交于A，B两点．若|AF|=3|BF|，则l的方程为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网