题目内容
19.在△ABC中,已知A(0,0),B(3,4),C(2,-1),H为△ABC的垂心,则H的坐标为($\frac{10}{11}$,$-\frac{2}{11}$).分析 由斜率公式和垂直关系可得AB和BC边的高线所在直线的方程,联立方程解方程组可得.
解答 解:由题意可得AB的斜率kAB=$\frac{4}{3}$,
∴AB边的高线的斜率k=$-\frac{3}{4}$,
∵AB边的高线过C(2,-1),
∴AB边的高线所在直线的方程为y+1=$-\frac{3}{4}$(x-2),①
同理可得BC边高线所在直线方程为y=-$\frac{1}{5}$x,②
联立①②可解得$\left\{\begin{array}{l}{x=\frac{10}{11}}\\{y=-\frac{2}{11}}\end{array}\right.$,即垂心H的坐标为($\frac{10}{11}$,$-\frac{2}{11}$)
故答案为:($\frac{10}{11}$,$-\frac{2}{11}$)
点评 本题考查直线的一般式方程和垂直关系,涉及方程组的解法,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若a>b>c,则下列不等式中正确的是( )
| A. | ac>bc | B. | ac2>bc2 | C. | b(a-b)>c(a-b) | D. | |ac|>|bc| |
14.已知△ABC的面积S=$\frac{\sqrt{3}}{4}$(a2+b2-c2),则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
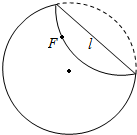 准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?
准备一张圆形纸片,在圆内任取不同于圆心的一点F,将纸片折起,使圆周过点F(如图),然后将纸片展开,就得到一条折痕L(为了看清楚,可以把直线L画出来),这样继续下去得到若干折痕.观察这些折痕围成的轮廓,它们形成了什么曲线?