题目内容
8.已知函数f(x)=$\sqrt{1-ax}$,求函数f(x)的定义域.分析 由根式内部的代数式大于等于0,然后对a分类求解得答案.
解答 解:由1-ax≥0,得ax≤1,
若a<0,则x≥$\frac{1}{a}$;
若a=0,则x∈R;
若a>0,则x$≤\frac{1}{a}$.
∴当a<0时,函数f(x)的定义域为[$\frac{1}{a}$,+∞);
当a=0时,函数f(x)的定义域为R;
当a>0时,函数f(x)的定义域为(-∞,$\frac{1}{a}$].
点评 本题考查函数的定义域及其求法,考查了分类讨论的数学思想方法,是基础题.

练习册系列答案
相关题目
18.已知函数f(x)=|x-4|+|x+4|,g(x)=|x-4|-|x+4|,下列结论正确的是( )
| A. | f(x)与g(x)既有最大值,又有最小值 | |
| B. | f(x)有最小值,没有最大值;g(x)有最大值,没有最小值 | |
| C. | f(x)有最小值,没有最大值;g(x)既有最大值,又有最小值 | |
| D. | f(x)既有最大值,又有最小值;g(x)有最小值,没有最大值 |
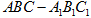 中,
中, 是
是 的中点.
的中点.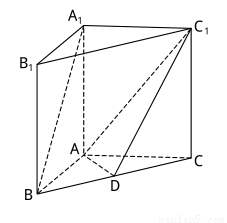
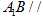 平面
平面 ;
; ,
, ,
,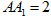 ,求几何体
,求几何体 的体积
的体积