题目内容
【题目】如图,在四棱锥P﹣ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.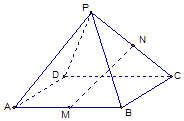
(1)求证:MN∥平面PAD.
(2)若PA=AD=2a,MN与PA所成的角为30°.求MN的长.
【答案】
(1)
证明:取PD的中点E,连接EN、EA,
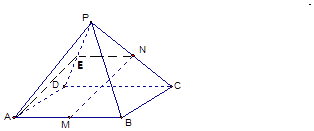
∵M,N分别是AB,PC的中点,ABCD是平行四边形,
∴EN ![]() AM,∴四边形ENMA为平行四边形
AM,∴四边形ENMA为平行四边形
∴MN∥AE,
∵MN平面PAD,AE平面PAD,
∴MN∥平面PAD
(2)
解:∵E是PD中点,PA=AD=2a,
∴AE是∠PAD的平分线,
∵MN与PA所成的角为30°,MN∥AE,∴∠PAE=30°,
∴△PAD是等边三角形,
∴MN=PE= ![]() =
= ![]() a.
a.
【解析】(1)取PD的中点E,连接EN、EA,推导出四边形ENMA为平行四边形,从而MN∥AE,由此能证明MN∥平面PAD.(2)推导出△PAD是等边三角形,MN=PE,由此能求出结果.
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面平行的判定的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目