题目内容
【题目】如图1所示,在边长为24的正方形![]() 中,点
中,点![]() 在边
在边![]() 上,且
上,且![]() ,
, ![]() ,作
,作![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,将该正方形沿
,将该正方形沿![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)416.
【解析】试题分析:
(1)由题意可证得AB⊥BC,AB⊥BB1,利用线面垂直的判定定理即可证得AB⊥平面BCC1B1.
(2)利用多面体的几何特征可得多面体A1B1C1-APQ的体积V=VABC-A1B1C1-VA-CQPB=416
试题解析:
(1)由题知,在图2中,AB=6,BC=8,CA=10,
∴AB2+BC2=CA2,∴AB⊥BC.
又∵AB⊥BB1,BC∩BB1=B,∴AB⊥平面BCC1B1.
(2)由题易知三棱柱ABC-A1B1C1的体积为![]() ×6×8×24=576.
×6×8×24=576.
∵在图1中,△ABP和△ACQ都是等腰直角三角形,
∴AB=BP=6,AC=CQ=14,
∴VA-CQPB=![]() ×S四边形CQPB×AB=
×S四边形CQPB×AB=![]() ×
×![]() ×(6+14)×8×6=160.
×(6+14)×8×6=160.
∴多面体A1B1C1-APQ的体积V=VABC-A1B1C1-VA-CQPB=576-160=416

 孟建平小学滚动测试系列答案
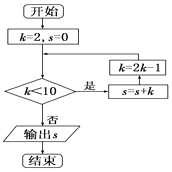
孟建平小学滚动测试系列答案【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |

(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)若成绩在80.5~90.5分的学生可以获得二等奖,问获得二等奖的学生约为多少人?
【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.