题目内容
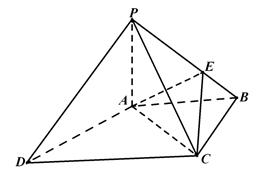
如图,四棱锥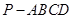 中,
中,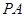 ⊥底面
⊥底面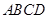 ,底面
,底面 为梯形,
为梯形,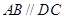 ,
,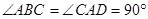
 ,且
,且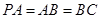 ,点
,点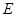 是棱
是棱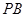 上的动点.
上的动点.
(Ⅰ)当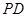 ∥平面
∥平面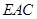 时,确定点
时,确定点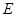 在棱
在棱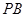 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角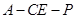 的余弦值.
的余弦值.
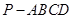 中,
中,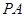 ⊥底面
⊥底面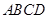 ,底面
,底面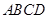 为梯形,
为梯形,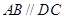 ,
,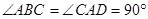
 ,且
,且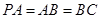 ,点
,点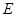 是棱
是棱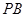 上的动点.
上的动点.(Ⅰ)当
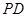 ∥平面
∥平面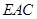 时,确定点
时,确定点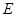 在棱
在棱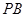 上的位置;
上的位置;(Ⅱ)在(Ⅰ)的条件下,求二面角
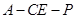 的余弦值.
的余弦值.
(Ⅰ)在梯形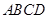 中,由
中,由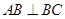 ,
,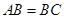 ,得
,得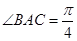 ,
,
∴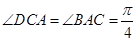 .又
.又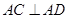 ,故
,故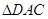 为等腰直角三角形.
为等腰直角三角形.
∴ .
.
连接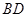 ,交
,交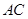 于点
于点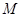 ,则
,则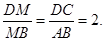
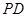 ∥平面
∥平面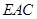 ,又平面
,又平面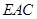
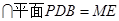 ,∴
,∴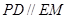 .
.
在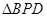 中,
中,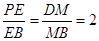 ,
,
即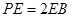 时,
时,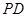 ∥平面
∥平面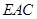 . 6分
. 6分
(Ⅱ)方法一:在等腰直角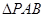 中,取
中,取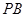 中点
中点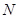 ,连结
,连结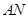
 ,则
,则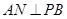 .∵平面
.∵平面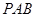 ⊥平面
⊥平面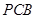 ,且平面
,且平面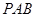
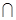 平面
平面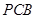 =
=
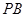 ,∴
,∴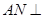 平面
平面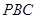 .
.
在平 面
面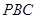 内,过
内,过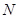 作
作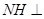 直线
直线 于
于 ,连结
,连结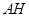 ,由
,由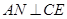 、
、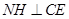 ,得
,得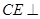 平面
平面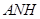 ,故
,故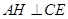 .∴
.∴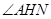 就是二面角
就是二面角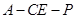
 的平面角.
的平面角.
在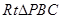 中,设
中,设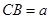 ,则
,则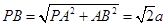 ,
,
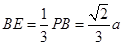 ,
,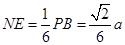 ,
,
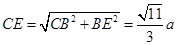 ,
,
由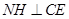 ,
,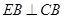 可知:
可知: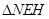 ∽
∽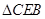 ,∴
,∴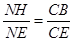 ,
,
代入解得: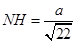 .
.
在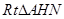 中,
中,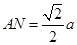 ,∴
,∴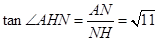 ,
,
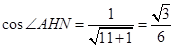 .
.
∴二面角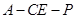 的余弦值为
的余弦值为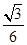 . 12分
. 12分
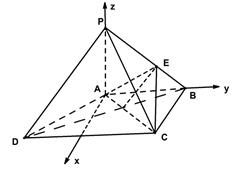
方法二:以
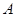 为原点,
为原点,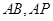 所在直线
所在直线 分别为
分别为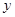 轴、
轴、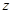 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
设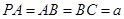 ,则
,则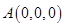 ,
,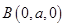 ,
,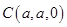 ,
,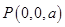 ,
,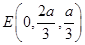 .
.
设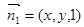 为平面
为平面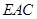 的一个法向量,则
的一个法向量,则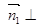
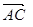 ,
,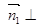
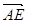 ,∴
,∴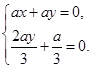 ,解得
,解得 ,∴
,∴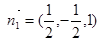 .
.
设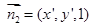 为平面
为平面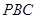 的一个法向量,则
的一个法向量,则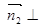
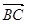 ,
,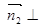
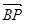 ,
,
又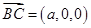 ,
,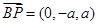 ,∴
,∴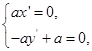 ,解得
,解得
∴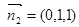 .
.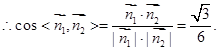
∴二面角
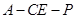 的余弦值为
的余弦值为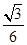 . 12分
. 12分
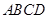 中,由
中,由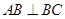 ,
,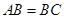 ,得
,得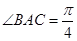 ,
,
∴
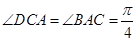 .又
.又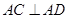 ,故
,故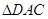 为等腰直角三角形.
为等腰直角三角形.∴
 .
. 连接
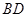 ,交
,交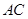 于点
于点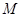 ,则
,则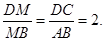
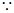
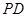 ∥平面
∥平面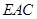 ,又平面
,又平面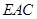
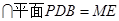 ,∴
,∴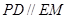 .
.在
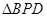 中,
中,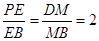 ,
,即
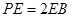 时,
时,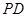 ∥平面
∥平面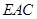 . 6分
. 6分(Ⅱ)方法一:在等腰直角
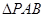 中,取
中,取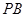 中点
中点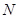 ,连结
,连结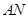
 ,则
,则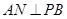 .∵平面
.∵平面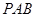 ⊥平面
⊥平面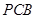 ,且平面
,且平面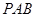
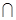 平面
平面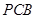 =
=
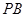 ,∴
,∴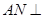 平面
平面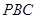 .
.在平
 面
面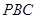 内,过
内,过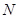 作
作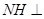 直线
直线 于
于 ,连结
,连结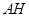 ,由
,由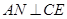 、
、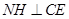 ,得
,得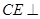 平面
平面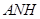 ,故
,故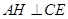 .∴
.∴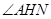 就是二面角
就是二面角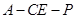
 的平面角.
的平面角. 在
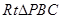 中,设
中,设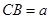 ,则
,则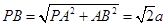 ,
,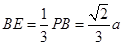 ,
,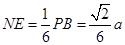 ,
,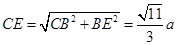 ,
,由
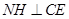 ,
,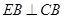 可知:
可知: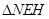 ∽
∽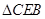 ,∴
,∴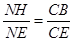 ,
,代入解得:
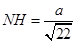 .
.在
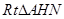 中,
中,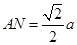 ,∴
,∴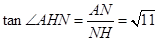 ,
,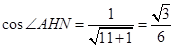 .
.∴二面角
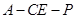 的余弦值为
的余弦值为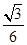 . 12分
. 12分方法二:以

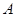 为原点,
为原点,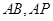 所在直线
所在直线 分别为
分别为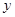 轴、
轴、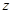 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.设
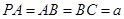 ,则
,则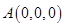 ,
,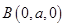 ,
,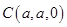 ,
,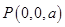 ,
,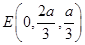 .
.设
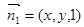 为平面
为平面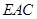 的一个法向量,则
的一个法向量,则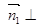
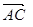 ,
,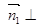
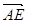 ,∴
,∴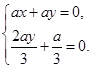 ,解得
,解得 ,∴
,∴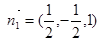 .
. 设
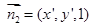 为平面
为平面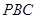 的一个法向量,则
的一个法向量,则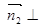
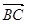 ,
,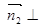
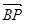 ,
,又
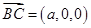 ,
,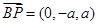 ,∴
,∴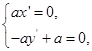 ,解得
,解得
∴
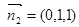 .
.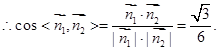
∴二面角

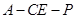 的余弦值为
的余弦值为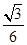 . 12分
. 12分略

练习册系列答案
相关题目
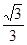
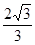
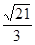
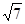
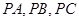 两两垂直,且
两两垂直,且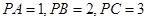 ,则三棱锥
,则三棱锥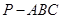 的外接球的表面积为( )
的外接球的表面积为( )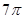
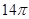
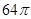

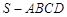 ,底面四边形ABCD满足条件
,底面四边形ABCD满足条件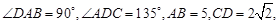 ,
,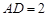 ,侧面SAD垂直于底面ABCD,
,侧面SAD垂直于底面ABCD,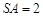 ,
,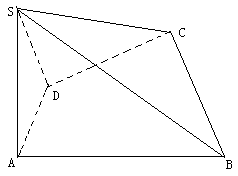
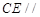 平面SAD,求
平面SAD,求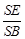 的值;
的值;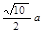
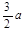
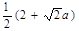

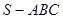 中,
中, 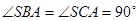 , △
, △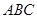 是斜边
是斜边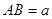 的等腰直角三角形, 则以下结论中: ① 异面直线
的等腰直角三角形, 则以下结论中: ① 异面直线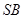 与
与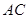 所成的角为
所成的角为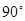 ; ② 直线
; ② 直线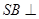 平面
平面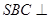 面
面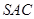 ; ④ 点
; ④ 点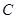 到平面
到平面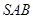 的距离是
的距离是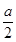 . 其中正确结论的序号是 ______
. 其中正确结论的序号是 ______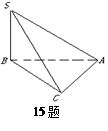
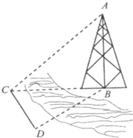
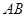 时,可以选与塔底
时,可以选与塔底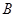 在同一水平面内的两个测点
在同一水平面内的两个测点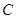 与
与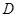 ,测得
,测得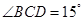 .
.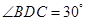 ,
,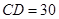 米,并在点
米,并在点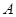 的仰角为
的仰角为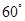 ,则塔高
,则塔高