题目内容
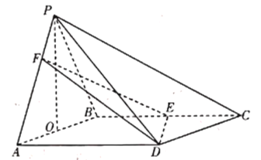
【题目】如图,已知边长为2的菱形ABCD,其中∠BAD=120°,AE∥CF,CF⊥平面ABCD,![]() ,
,![]() .
.
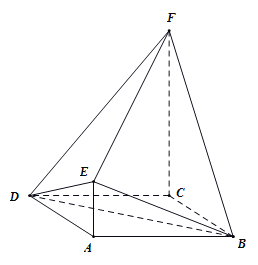
(1)求证:平面BDE⊥平面BDF;
(2)求二面角D﹣EF﹣B的大小.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证明BD⊥CF,BD⊥AC,推出BD⊥平面ACFE,得到OF⊥BD,由已知推出AE⊥平面ABCD,得AE⊥AO且FC⊥CO,在直角梯形![]() 中可证明OF⊥OE,从而得OF⊥平面BDE,然后证得结论面面垂直.
中可证明OF⊥OE,从而得OF⊥平面BDE,然后证得结论面面垂直.
(2)以OA,OB所在的直线分别为x轴,y轴,过O做垂直于平面ABCD的为z轴建立空间直角坐标系.求出平面DEF的一个法向量,平面BEF的一个法向量,通过空间向量的数量积求解二面角D﹣EF﹣B的大小.
(1)证明:因为AE∥CF,所以A、C、F、E四点共面.
又CF⊥平面ABCD,而BD平面ABCD,所以BD⊥CF,
由菱形ABCD,所以BD⊥AC,
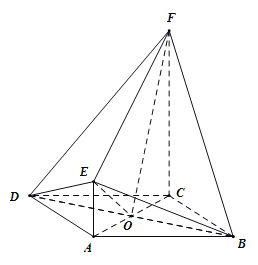
且CF∩AC=C,所以,BD⊥平面ACFE,
令BD∩AC=O,如图所示,OF平面ACFE,所以OF⊥BD,
因为AE∥CF且CF⊥平面ABCD,所以AE⊥平面ABCD,
则AE⊥AO且FC⊥CO,![]() ,
,![]() ,
,
由菱形ABCD且∠BAD=120,所以AO=OC=1,
故![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
所以![]() ,即OF⊥OE,
,即OF⊥OE,
又OE∩BD=O,所以OF⊥平面BDE,
又∵OF平面BDF,平面BDE⊥平面BDF.
(2)由菱形ABCD,所以BD⊥AC,以OA,OB所在的直线分别为x轴,y轴,
过O作垂直于平面ABCD的直线为z轴建立空间直角坐标系.则![]() 轴,
轴,![]() 轴,
轴,
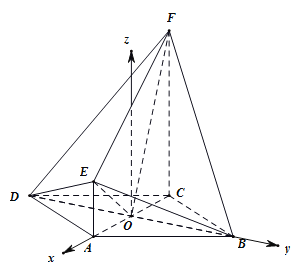
则![]() ,所以A(1,0,0),
,所以A(1,0,0),![]() ,
,![]() ,
,![]() ,
,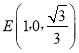 ,
,
所以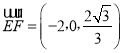 ,
,![]() ,
,![]() ,
,
令平面DEF的一个法向量为![]() ,且
,且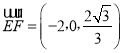 ,
,![]() ,
,
由![]() ,
,![]() ,所以
,所以![]() ,
,
由![]() ,
,![]() ,所以
,所以![]() ,即
,即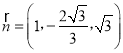 ,
,
令平面BEF的一个法向量为:![]() ,且
,且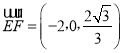 ,
,![]() ,
,
由![]() ,
,![]() ,所以
,所以![]() ,
,
由![]() ,
,![]() ,所以
,所以![]() ,即
,即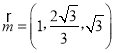 ,
,
所以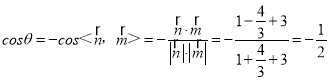 ,则
,则![]() ,
,
即二面角D﹣EF﹣B的大小为![]() .
.

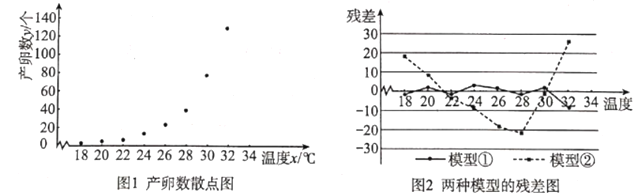
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为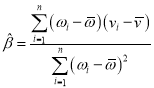 ,
,![]() .
.