题目内容
如图，ABCD、CDEF是两个边长都为
的正方形，且平面ABCD⊥平面CDEF，M、N分别是AB、AC的中点，H是DE上的一个动点。
(Ⅰ)求证：HN⊥AC；
(Ⅱ)当EH＝HD时，在AD上确定一点P，使得HP∥平面EMC.
解析： (Ⅰ)证明：连接BD、BE，
由ABCD是正方形，得AC⊥BD…………①，且交于N，
因为平面ABCD⊥平面CDEF，交线为CD，ED⊥CD，故ED⊥平面ABCD，…………4分
所以ED⊥AC…………②，又ED∩BD＝D………③，
由①②③知，AC⊥平面BDE
HN
平面BDE，故HN⊥AC ………………………………………………………………6分
(Ⅱ) EH＝HD时，H为DE的中点，取CD中点S，
连接HS、AH、AS，
则有HS∥EC、AS∥MC，又HS∩AS＝S，CE∩MC＝C，
故平面MCE∥平面ASH………………………10分
又AH平面ASH，所以AH∥平面MCE，
练习册系列答案
相关题目
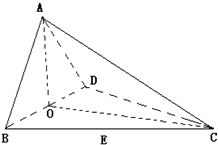如图四面体ABCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，
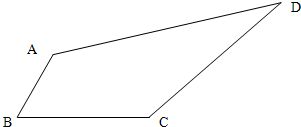如图四边形ABCD中，AB=2，BC=
（2013•镇江二模）（选修4-1 几何证明选讲）
, ∠DAB＝60°, 则梯形的高等于_____
.
AB,E是AB中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角PDEC的大小为120°.