Question

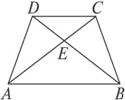
如图,梯形ABCD中,CD∥AB,AD=DC=CB=AB,E是AB中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角PDEC的大小为120°.

(1)求证:DE⊥PC;

(2)求直线PD与平面BCDE所成角的大小;

(3)求点D到平面PBC的距离.

Answer 1

(1)证明:连结AC交DE于F,连结PF.

∵CD∥AB,

∴∠BAC=∠ACD.

又∵AD=CD,

∴∠DAC=∠ACD.

∴∠BAC=∠DAC,即CA平分∠BAD.

∵△ADE是正三角形, ∴AC⊥DE,                                            

即PF⊥DE,CF⊥DE.∴DE⊥平面PCF.

∴DE⊥PC.                                                                  

(2)解:过P作PO⊥AC于O,连结OD.

设AD=DC=CB=a,则AB=2a.

∵DE⊥平面PCF,∴DE⊥PO.∴PO⊥平面BCDE.

∴∠PDO即为直线PD与平面BCDE所成的角.                                 

∵∠PFC是二面角PDEC的平面角,

∴∠PFO=60°.                                                              

在Rt△POF中,∵∠PFO=60°,PF=a,

∴PO=a.

在Rt△POD中,sin∠PDO==,

∴直线PD与平面BCDE所成角是arcsin.                                    

(3)解:∵DE∥BC,DE在平面PBC外,

∴DE∥平面PBC.∴点D到平面PBC的距离即为点F到平面PBC的距离.

过点F作FG⊥PC,垂足为G.

∵DE⊥平面PCF,∴BC⊥平面PCF.

∴平面PBC⊥平面PCF.∴FG⊥平面PBC.

∴FG的长即为点F到平面PBC的距离.                                      

在菱形ADCE中,AF=FC,

∴PF=CF=a.

∵∠PFC=120°,∴∠FPC=∠FCP=30°.

∴FG=PF=a.