题目内容
14.已知sin(3π-α)=$\sqrt{2}$sin(6π+β),$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),且0<α<π,0<β<π,求α和β的值.分析 由条件利用同角三角函数的基本关系、诱导公式求得cosα和cosβ的值,再结合角的范围得答案.
解答 解:由sin(3π-α)=$\sqrt{2}$sin(6π+β),得
sinα=$\sqrt{2}$sinβ ①,
由$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),得
$\sqrt{3}$cosα=$\sqrt{2}$cosβ ②,
①2+②2得,sin2α+3cos2α=2,即$co{s}^{2}α=\frac{1}{2}$,∴cos$α=±\frac{\sqrt{2}}{2}$,
∵0<α<π,∴α=$\frac{π}{4}$或$α=\frac{3π}{4}$;
当α=$\frac{π}{4}$时,由$\sqrt{3}$cosα=$\sqrt{2}$cosβ,得cosβ=$\frac{\sqrt{3}}{2}$,
∵0<β<π,∴$β=\frac{π}{6}$.
当$α=\frac{3π}{4}$时,由$\sqrt{3}$cosα=$\sqrt{2}$cosβ,得cosβ=-$\frac{\sqrt{3}}{2}$,
∵0<β<π,∴$β=\frac{5π}{6}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,体现了分类讨论的数学思想方法,属于基础题.

练习册系列答案
相关题目
5.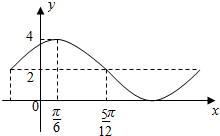 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )| A. | B=1 | B. | φ=$\frac{π}{6}$ | C. | ω=1 | D. | A=4 |