题目内容
给出下列五个命题:①若f′(x)=0,则函数y=f(x)在x=x处取得极值;
②若m≥-1,则函数
 的值域为R;
的值域为R;③“a=1”是“函数
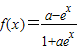 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.④函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑤“x1>1且x2>2”是“x1+x2>3且x1x2>2”的充要条件;
其中正确命题的个数是 .
【答案】分析:利用导数的概念,对数函数的性质,函数的对称性与充分条件的概念对四个选项逐一判断即可.
解答:解:对于①,若f(x)=x3,则f′(0)=0,而函数y=f(x)在x=0处取不能取得极值,故①错误;
对于②,若使f(x)=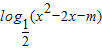 的值域为R,则△=4+4m≥0,
的值域为R,则△=4+4m≥0,
∴m≥-1,
故②正确;
对于③,若a=1,则f(-x)=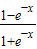 =
=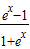 =-f(x),
=-f(x),
∴f(x)在定义域上是奇函数;反之,若f(-x)=-f(x),即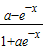 =-
=-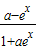 ,
,
整理得(a2-1)(e2x+1)=0,由于e2x+1>0,
∴a=±1,
∴“a=1”是“函数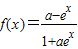 在定义域上是奇函数”的充分不必要条件,故③正确;
在定义域上是奇函数”的充分不必要条件,故③正确;
对于④,函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称是错误的;
对于⑤,“x1>1且x2>2”是“x1+x2>3且x1x2>2”的充分条件而非充要条件;故⑤错误.
综上所述,②③正确.
故答案为:②③.
点评:本题考查命题的真假判断与应用,考查函数的基本性质及充分条件,考查综合分析与应用的能力,属于难题.
解答:解:对于①,若f(x)=x3,则f′(0)=0,而函数y=f(x)在x=0处取不能取得极值,故①错误;
对于②,若使f(x)=
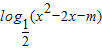 的值域为R,则△=4+4m≥0,
的值域为R,则△=4+4m≥0,∴m≥-1,
故②正确;
对于③,若a=1,则f(-x)=
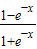 =
=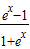 =-f(x),
=-f(x),∴f(x)在定义域上是奇函数;反之,若f(-x)=-f(x),即
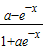 =-
=-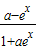 ,
,整理得(a2-1)(e2x+1)=0,由于e2x+1>0,
∴a=±1,
∴“a=1”是“函数
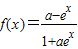 在定义域上是奇函数”的充分不必要条件,故③正确;
在定义域上是奇函数”的充分不必要条件,故③正确;对于④,函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称是错误的;
对于⑤,“x1>1且x2>2”是“x1+x2>3且x1x2>2”的充分条件而非充要条件;故⑤错误.
综上所述,②③正确.
故答案为:②③.
点评:本题考查命题的真假判断与应用,考查函数的基本性质及充分条件,考查综合分析与应用的能力,属于难题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目