题目内容
18.已知函数f(x)=$\frac{1}{2}$x2-$\frac{2}{3}$ax3,函数g(x)=f(x)+2ex(x-1),函数g(x)的导函数为g′(x).(1)当函数y=f(x)在区间(1,+∞)时为减函数,求a的范围;
(2)若a=e(e为自然对数的底数),
①求函数g(x)的单调区间;
②证明:g′(x)≥1+lnx.
分析 (1)求导得f′(x)=x-2ax2=x(-2ax+1),利用直线的性质,求a的范围.
(2)①求导,得g′(x)=x(1-2ex+2ex),只需判断后一表达式的正负.一般都是构造函数,利用求极值的方法判断.
②把恒成立问题转化为最值问题,通过求导,判断函数的极值,求出最值.
解答 解:(1)由函数y=f(x)在区间(1,+∞)时为减函数
∴f′(x)=x-2ax2=x(-2ax+1)≤0 x∈(1,+∞)
∴a>0且-2a×1+1≤0
∴a≥$\frac{1}{2}$
(2)①g(x)=$\frac{1}{2}$x2-$\frac{2}{3}$ex3+2ex(x-1)
∴g′(x)=x(1-2ex+2ex)
令h(x)=1-2ex+2ex
h′(x)=-2e+2ex=2(ex-e)
当x<1时,h′(x)<0,h(x)递减
当x>1时,h′(x)>0,h(x)递增
∴h(x)≥h(1)=1>0
∴当x>0时,g′(x)>0,g(x)递增
当x<0时,g′(x)<0,g(x)递减
②x(1-2ex+2ex)≥1+lnx x>0
∴1-2ex+2ex≥$\frac{1+lnx}{x}$
只需证$\frac{1+lnx}{x}$≤1
令M(x)=$\frac{1+lnx}{x}$
∴M′(x)=$\frac{-lnx}{{x}^{2}}$
当x∈(0,1),M′(x)>0,M(x)递增
当x∈(1,∞),M′(x)<0,M(x)递减
∴M(x)≤M(1)=1
∴1-2ex+2ex≥$\frac{1+lnx}{x}$
故g′(x)≥1+lnx.
点评 考察了复合函数的求导,极值的判定,恒成立问题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
3.直线y=kx+1与曲线y=ax3+lnx+b相切于点(1,5),则a-b=( )
| A. | -3 | B. | 2 | C. | 3 | D. | -2 |
7.若函数f(x)=loga(x2+$\frac{3}{2}$x)(a>0,a≠1)在区间($\frac{1}{2}$,+∞)内恒有f(x)>0,则f(x)的单调增区间为( )
| A. | (0,+∞) | B. | (2,+∞) | C. | (1,+∞) | D. | ($\frac{1}{2}$,+∞) |
8.两个线性相关变量x与y的统计数据如表:
其回归直线方程是$\widehat{y}$=$\widehat{b}$x+40,则相应于点(9,11)的残差为( )
| x | 9 | 9.5 | 10 | 10.5 | 11 |
| y | 11 | 10 | 8 | 6 | 5 |
| A. | 0.1 | B. | 0.2 | C. | -0.2 | D. | -0.1 |
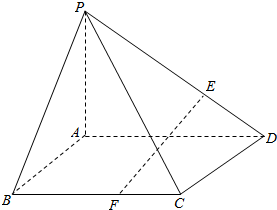 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a.点E、F分别在PD、BC上,且PE:ED=BF:FC