题目内容
7.函数f(x)=x3+ax2+bx+1在x=1时有极值4,那么a,b的值分别为a=-5,b=7.分析 先求出函数的导函数f′(x),然后根据在x=1时f(x)有极值4,得到$\left\{\begin{array}{l}{f′(1)=0}\\{f(1)=4}\end{array}\right.$,求出满足条件a,b的值.
解答 解:对函数f(x)求导得 f′(x)=3x2+2ax+b,
又∵在x=1时f(x)有极值4,
∴$\left\{\begin{array}{l}{f′(1)=3+2a+b=0}\\{f(1)=1+a+b+2=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-5}\\{b=7}\end{array}\right.$,
故答案为:a=-5,b=7.
点评 本题主要考查了函数在某点取得极值的条件,以及考查利用函数的极值存在的条件求参数的能力,属于基础题.

练习册系列答案
相关题目
18.甲、乙两人参加某单位招聘面试测试,每次测试从试题库随机用一套试题,他们参加的5项测试成绩记录如下:
(1)用茎叶图表示甲、乙这5项测试成绩;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
2.若命题p:0是偶数,命题q:2是3的约数.则下列命题中为真的是( )
| A. | p且q | B. | p或q | C. | 非p | D. | 非p且非q |
19.如图三角形OAB为用斜二测画法所画的直观图,其原来平面图形的面积是( )
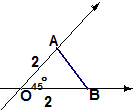

| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
16.已知$tanα=\frac{1}{2}$,则$\frac{{2{{cos}^2}\frac{α}{2}-sinα-1}}{{\sqrt{2}sin(\frac{π}{4}+α)}}$的值为( )
| A. | $\frac{4}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
