题目内容
 (2011•大连二模)如图,在棱长AB=AD=2,AA1=3的长方体ABCD-A1B1C1D1中,点E是平面BCC1B1内动点,点F是CD的中点.
(2011•大连二模)如图,在棱长AB=AD=2,AA1=3的长方体ABCD-A1B1C1D1中,点E是平面BCC1B1内动点,点F是CD的中点.(Ⅰ)试确定E的位置,使D1E⊥平面AB1F;
(Ⅱ)求平面AB1F与平面ABB1A1所成的锐二面角的大小.
分析:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设E(2,y,z)利用空间向量方法
将D1E⊥平面AB1F转化为
,进行代数运算,解出y,z.确定出E位置.
(Ⅱ)方法一:当D1E⊥平面AB1F时,平面AB1F的法向量为
,又
是平面A1AB1的法向量,利用两法向量夹角求出平面AB1F与平面ABB1A1所成的锐二面角的大小.
法二:取AB的中点G,可证:FG⊥平面ABB1A1,过点G作GH⊥AB1于H点,连接FH,则FH⊥AB1,所以∠GHF为所求二面角的平面角,在△GHF中求解即可.
将D1E⊥平面AB1F转化为
|
(Ⅱ)方法一:当D1E⊥平面AB1F时,平面AB1F的法向量为
| D1E |
| AD |
法二:取AB的中点G,可证:FG⊥平面ABB1A1,过点G作GH⊥AB1于H点,连接FH,则FH⊥AB1,所以∠GHF为所求二面角的平面角,在△GHF中求解即可.
解答: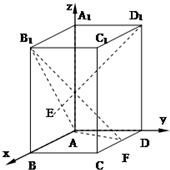 解:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
解:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),
设E(2,y,z),则
=(2,y-2,z-3),
=(1,2,0),
=(2,0,3).(4分)
由D1E⊥平面AB1F∴
∴
∴
∴E(2,1,
) 为所求. …(6分)
(Ⅱ)方法一:当D1E⊥平面AB1F时,
=(2,-1,-
),
又
是平面A1AB1的法向量,
且
=(0,2,0).(8分)cos<
,
>=
=
=-
.
∴面AB1F与平面ABB1A1所成的锐二面角的大小arccos
.(12分)
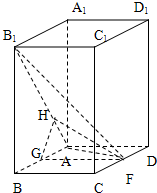 方法二:取AB的中点G,可证:FG⊥平面ABB1A1,
方法二:取AB的中点G,可证:FG⊥平面ABB1A1,
过点G作GH⊥AB1于H点,连接FH,则FH⊥AB1,
所以∠GHF为所求二面角的平面角.…(9分)
在△GHF中,FG=2,FHFH=1×tan∠B1AB=
tan∠GHF=
=
.
∴面AB1F与平面ABB1A1所成的锐二面角的大小arccos
.(12分)
 解:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
解:(Ⅰ)以A为原点,AB、AD、AA1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),
设E(2,y,z),则
| D1E |
| AF |
| AB1 |
由D1E⊥平面AB1F∴
|
|
|
∴E(2,1,
| ,5 |
| 3 |
(Ⅱ)方法一:当D1E⊥平面AB1F时,
| D1E |
| 4 |
| 3 |
又
| AD |
且
| AD |
| AD |
| D1E |
| ||||
|
|
2×0+(-1)×2+(-
| ||||
2×
|
3
| ||
| 61 |
∴面AB1F与平面ABB1A1所成的锐二面角的大小arccos
3
| ||
| 61 |
 方法二:取AB的中点G,可证:FG⊥平面ABB1A1,
方法二:取AB的中点G,可证:FG⊥平面ABB1A1,过点G作GH⊥AB1于H点,连接FH,则FH⊥AB1,
所以∠GHF为所求二面角的平面角.…(9分)
在△GHF中,FG=2,FHFH=1×tan∠B1AB=
| 3 | ||
|
| GF |
| GH |
2
| ||
| 3 |
∴面AB1F与平面ABB1A1所成的锐二面角的大小arccos
3
| ||
| 61 |
点评:本题考查空间直线和平面垂直的判定.考查空间想象、推理论证能力.利用空间向量的方法,能降低空间想象难度,思,将几何元素位置关系转化为代数运算表示.是人们研究解决几何体问题又一有力工具.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 (2011•大连二模)选修4-1:几何证明选讲
(2011•大连二模)选修4-1:几何证明选讲 (2011•大连二模)某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
(2011•大连二模)某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( ) (2011•大连二模)一个几何体的三视图为如图所示的三个直角三角形,则这个几何体的体积为
(2011•大连二模)一个几何体的三视图为如图所示的三个直角三角形,则这个几何体的体积为