题目内容
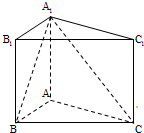如图，在直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=| 3 |
| π |
| 3 |
（Ⅰ）证明：AB⊥A1C；
（Ⅱ）求二面角A-A1C-B的正弦值．
分析：（I）由已知中AB=1，AC=AA1=
，∠ABC=
．我们易得AB⊥AC，又由直三棱柱的几何特征得AA1⊥AB，结合线面垂直的判定定理，可得AB⊥平面AA1C，进而根据线面垂直的性质，即可得到AB⊥A1C；
（Ⅱ）取A1C中点D，连AD，BD，由已知易得AD⊥A1C，结合三垂线定理，我们可得∠BDA为二面角A-A1C-B的平面角，解三角形BDA，即可求出二面角A-A1C-B的正弦值．
| 3 |
| π |
| 3 |
（Ⅱ）取A1C中点D，连AD，BD，由已知易得AD⊥A1C，结合三垂线定理，我们可得∠BDA为二面角A-A1C-B的平面角，解三角形BDA，即可求出二面角A-A1C-B的正弦值．
解答：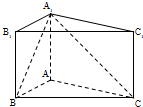
解：（Ⅰ）在△ABC中，AB=1，AC=
，∠ABC=
∴AB⊥AC，又AA1⊥AB，则AB⊥平面AA1C
∵A1C在平面ABC内的射影为AC，∴AB⊥A1C …（6分）
（Ⅱ）取A1C中点D，连AD，BD∵AA1=AC=
∴AD⊥A1C，且AD=
，
由三垂线定理得 BD⊥A1C
∴∠BDA为二面角A-A1C-B的平面角．
∴tan∠BDA=
=
，∴sin∠BDA=
∴二面角A-A1C-B的正弦值为
． …（12分）
解：（Ⅰ）在△ABC中，AB=1，AC=| 3 |
| π |
| 3 |
∴AB⊥AC，又AA1⊥AB，则AB⊥平面AA1C
∵A1C在平面ABC内的射影为AC，∴AB⊥A1C …（6分）
（Ⅱ）取A1C中点D，连AD，BD∵AA1=AC=
| 3 |
∴AD⊥A1C，且AD=
| ||
| 2 |
由三垂线定理得 BD⊥A1C
∴∠BDA为二面角A-A1C-B的平面角．
∴tan∠BDA=
| AB |
| AD |
| ||
| 3 |
| ||
| 5 |
∴二面角A-A1C-B的正弦值为
| ||
| 5 |
点评：本题考查的知识点是直线与平面垂直的性质，二面角的平面角及求法，其中（I）的关键，是要根据已知条件及三棱柱的几何特征得到线面垂直的条件，（II）的关键是找出二面角的平面角．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
