题目内容
已知集合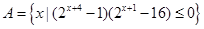 与
与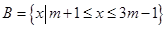 分别是函数
分别是函数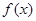 的定义域与值域.
的定义域与值域.
(1)求集合 ;
;
(2)当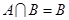 时,求实数
时,求实数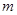 的取值范围.
的取值范围.
(1)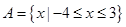 ;(2)
;(2)
解析试题分析:(1)从集合A中的元素特征条件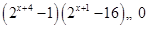 确定
确定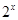 的范围,从而可求出集合A元素
的范围,从而可求出集合A元素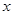 的范围,求出集合A;(2)由条件
的范围,求出集合A;(2)由条件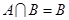 可知集合B是集合A的子集,又由已知条件得集合A是函数
可知集合B是集合A的子集,又由已知条件得集合A是函数 的定义域,所以
的定义域,所以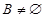 ,故集合B中元素的范围不小于集合A中元素的范围,列出不等式组,可求出实数
,故集合B中元素的范围不小于集合A中元素的范围,列出不等式组,可求出实数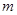 的取值范围.
的取值范围.
试题解析:(1)由 可化为
可化为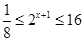
则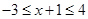 得
得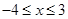
故集合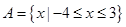 6分
6分
(2)∵集合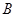 为函数的值域,∴
为函数的值域,∴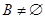
∵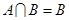 ,∴
,∴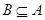 8分
8分
∴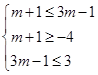 ,得
,得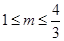
故实数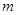 的取值范围为
的取值范围为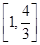 12分
12分
考点:1.集合的关系、运算;2.指数幂不等式的求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
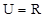 ,且A=
,且A=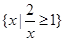 ,
,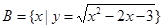 ,求
,求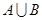 和
和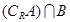 .
.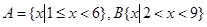
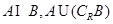
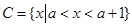 ,若
,若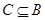 ,求实数
,求实数 的取值范围。
的取值范围。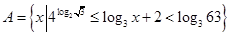 ,函数
,函数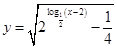 的定义域为
的定义域为
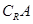 ;
; 。
。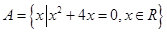 ,
,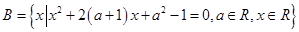 ,若
,若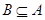 ,求实数
,求实数 的取值范围.
的取值范围.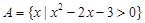 ,
,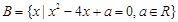 .
.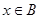 ,使得
,使得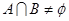 ,求
,求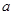 的取值范围;
的取值范围;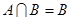 ,求
,求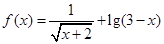 的定义域为集合A,集合B={x|-2<x<a}.
的定义域为集合A,集合B={x|-2<x<a}.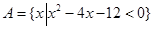 ,B={x|| x-m|≥1};命题p:x∈A,命题q:x∈B ,并且命题p是命题q的充分条件,求实数m的取值范围.
,B={x|| x-m|≥1};命题p:x∈A,命题q:x∈B ,并且命题p是命题q的充分条件,求实数m的取值范围.