题目内容
已知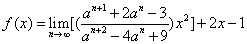
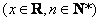 ,设
,设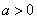 ,
,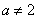 .
.
(Ⅰ)求出函数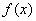 的解析式;
的解析式;
(Ⅱ)是否存在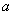 使得函数
使得函数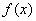 能以
能以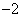 为其最小值?若能,求出对应的
为其最小值?若能,求出对应的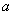 的取值或取值范围;若不能,试说明理由.
的取值或取值范围;若不能,试说明理由.
【答案】
(Ⅰ)∵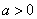 ,
,
∴当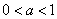 时
时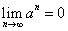 ,
,
∴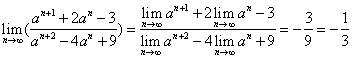 ,
,
此时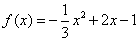 ,函数图象开口向下,没有最小值; …………3分
,函数图象开口向下,没有最小值; …………3分
当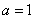 时,
时,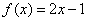 ,函数单调递增,此时也没有最小值; …………5分
,函数单调递增,此时也没有最小值; …………5分
当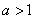 且
且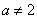 时
时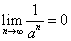 ,
,
∴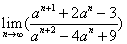
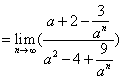
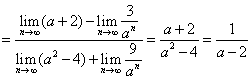 ,
,
此时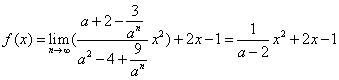 ; …………8分
; …………8分
(Ⅱ)若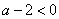 即
即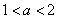 时,函数
时,函数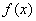 开口向下,没有最小值,
开口向下,没有最小值,
而当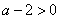 即
即 时,函数
时,函数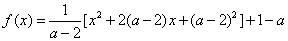 ,
,
当且仅当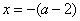 时有最小值
时有最小值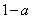 ,
,
令 ,则
,则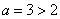 ,
,
∴存在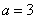 恰使函数
恰使函数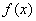 以
以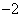 为其最小值. …………12分
为其最小值. …………12分
本题考查极限的概念、数列极限的求法、重要极限的应用、二次函数的最值及分类讨论的思想方法,属易错题、难题

练习册系列答案
相关题目
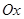 中,已知曲线
中,已知曲线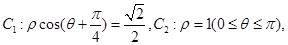
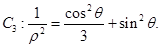 设
设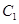 与
与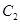 交于点
交于点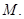
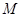 的极坐标;
的极坐标;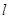 过点
过点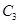 交于两个不同的点
交于两个不同的点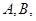 求
求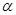
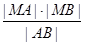 的最小值.
的最小值. ,设命题
,设命题 函数
函数 在R上单调递增;命题
在R上单调递增;命题 不等式
不等式 对任意
对任意 恒成立。若
恒成立。若 且
且 为假,
为假, 的取值范围。
的取值范围。 ,
,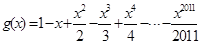 ,设
,设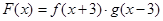 ,且函数
,且函数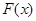 的零点均在区间
的零点均在区间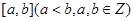 内,则
内,则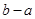 的最小值为____▲_____.
的最小值为____▲_____.