题目内容
已知问题“设正数x,y满足
+
=1,求x+y的最值”有如下解法;
设
=cos2α,
=sin2α,α∈(0,
),
则x=sec2α=1+tan2α,y=2csc2α=2(1+cot2α),
所以,x+y=3+tan2α+2cot2α=3+tan2+
≥3+2
,等号成立当且仅当tan2α=
,即tan2α=
,此时x=1+
,y=2+
.
(1)参考上述解法,求函数y=
+2
的最大值.
(2)求函数y=2
-
(x≥0)的最小值.
| 1 |
| x |
| 2 |
| y |
设
| 1 |
| x |
| 2 |
| y |
| π |
| 2 |
则x=sec2α=1+tan2α,y=2csc2α=2(1+cot2α),
所以,x+y=3+tan2α+2cot2α=3+tan2+
| 2 |
| tan2α |
| 2 |
| 2 |
| tan2α |
| 2 |
| 2 |
| 2 |
(1)参考上述解法,求函数y=
| 1-x |
| x |
(2)求函数y=2
| x+1 |
| x |
分析:(1)令
=cosα,
= sinα,α∈(0,
),y=cosα+2snα=
sin(α+θ),结合正弦函数的性质可求函数的最大值
(2)令
=secα,
=tanα,α∈(0,
),则y=2secα-tanα=
-
=
=-
,设k=
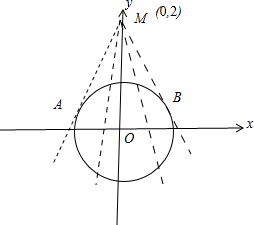
可以看成在单位圆(在第一象限的
圆周)上任取一点(cosα,sinα)与M(0,2)点的连线的斜率,结合图象可求最小值
| 1-x |
| x |
| π |
| 2 |
| 5 |
(2)令
| x+1 |
| x |
| π |
| 2 |
| 2 |
| cosα |
| sinα |
| cosα |
| 2-sinα |
| cosα |
| sinα-2 |
| cosα-0 |
| sinα-2 |
| cosα-0 |
| 1 |
| 4 |
解答:解:(1)令
=cosα,
= sinα,α∈(0,
)
y=cosα+2sinα=
sin(α+θ)(θ为辅助角)
函数的最大值
(2)令
=secα,
=tanα,α∈(0,
)
y=2secα-tanα=
-
=
=-
设k=
可以看成在单位圆(在第一象限的
圆周)上任取一点(cosα,sinα)与M(0,2)点的连线的斜率
结合图象可知,在MB位置时,函数斜率有最小值,此时直线MB与圆相切,此时斜率最大即-
取得最小值
设MB的直线为y=kx+2即kx-y-2=0
由直线与圆相切可得圆心(0,0)到直线MB的距离等于半径,即1=
∴k=
(舍)或k=-
∴-
取得最小值为
即y=2
-
的最小值
| 1-x |
| x |
| π |
| 2 |
y=cosα+2sinα=
| 5 |
函数的最大值
| 5 |
(2)令
| x+1 |
| x |
| π |
| 2 |
y=2secα-tanα=
| 2 |
| cosα |
| sinα |
| cosα |
| 2-sinα |
| cosα |
| sinα-2 |
| cosα-0 |
设k=
| sinα-2 |
| cosα-0 |
| 1 |
| 4 |
结合图象可知,在MB位置时,函数斜率有最小值,此时直线MB与圆相切,此时斜率最大即-
| sinα-2 |
| cosα |
设MB的直线为y=kx+2即kx-y-2=0
由直线与圆相切可得圆心(0,0)到直线MB的距离等于半径,即1=
| 2 | ||
|
∴k=
| 3 |
| 3 |
∴-
| sinα-2 |
| cosα |
| 3 |
即y=2
| x+1 |
| x |
| 3 |

点评:本题主要考查了三角函数的换元在求解函数的最值中的应用,(1)主要利用了辅助角公式及正弦函数的性质,(2)是构思非常巧妙的试题,注意题目中的几何意义的应用及求解圆的切线方程的求解,是一道好题

练习册系列答案
相关题目