题目内容
已知{an}是各项都为正数的等比数列,数列{bn}满足bn=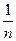 [lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
[lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
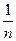 [lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
[lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.k=1时,{bn}成等差数列.
假设存在正数k,使得{bn}成等差数列.
设数列{an}的公比为q,则an=a1qn-1.
而bn=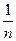 [lga1+lga2+lga3+…+lg(kan)]
[lga1+lga2+lga3+…+lg(kan)]
=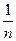 lg(ka1·a2·a3·…·an)
lg(ka1·a2·a3·…·an)
=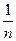 lg(k·a1n·
lg(k·a1n·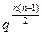 )
)
=lga1+(n-1)lg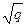 +lg
+lg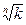 .
.
∴bn+1-bn=(lga1+nlg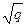 +lg
+lg )-[lga1+(n-1)lg
)-[lga1+(n-1)lg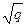 +lg
+lg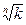 ]
]
=lg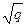 +lg
+lg -lg
-lg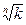 .
.
若{bn}为等差数列,当且仅当lg -lg
-lg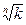 =0,
=0,
即lg =lg
=lg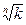 ,
, =
=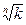 ,
,
∴k=1.
因此当k=1时,{bn}成等差数列.
设数列{an}的公比为q,则an=a1qn-1.
而bn=
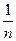 [lga1+lga2+lga3+…+lg(kan)]
[lga1+lga2+lga3+…+lg(kan)]=
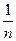 lg(ka1·a2·a3·…·an)
lg(ka1·a2·a3·…·an)=
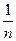 lg(k·a1n·
lg(k·a1n·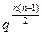 )
)=lga1+(n-1)lg
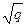 +lg
+lg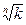 .
.∴bn+1-bn=(lga1+nlg
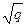 +lg
+lg )-[lga1+(n-1)lg
)-[lga1+(n-1)lg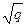 +lg
+lg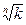 ]
]=lg
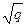 +lg
+lg -lg
-lg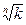 .
.若{bn}为等差数列,当且仅当lg
 -lg
-lg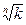 =0,
=0,即lg
 =lg
=lg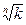 ,
, =
=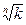 ,
,∴k=1.
因此当k=1时,{bn}成等差数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
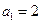 ,
,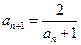 ,
,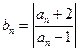 ,
,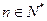 ,则数列
,则数列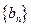 的通项公式
的通项公式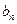 = 。
= 。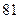
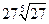
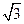
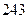
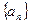 与等比数列
与等比数列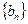 中,
中,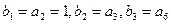 ,求
,求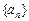 的各项均为
的各项均为 正数,公比
正数,公比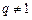 ,设
,设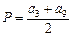 ,
, ,
,