题目内容
【题目】(2015·湖南)设数列{an}的前n项和为Sn , 已知a1=1, a2=2,且an+1=3Sn-Sn+1+3(n![]() )
)
(1)证明:an+2=3an;
(2)求Sn
【答案】
(1)
略。
(2)
Sn=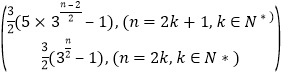
【解析】(I)由条件,对任意n![]() , 有an+2=3Sn-Sn+1+3(n
, 有an+2=3Sn-Sn+1+3(n![]() ),因而对任意an+1=3Sn-1-Sn+3, (n
),因而对任意an+1=3Sn-1-Sn+3, (n![]() ), 两式相减可得an+2-an+1=3an-an+1, 即an+2=3an(n≥2),又a1=1, a2=2,所以a3=3S1-S2+3=3a1-(a1+a2)+3=3a1, 故对一切n
), 两式相减可得an+2-an+1=3an-an+1, 即an+2=3an(n≥2),又a1=1, a2=2,所以a3=3S1-S2+3=3a1-(a1+a2)+3=3a1, 故对一切n![]() , an+2=3an。
, an+2=3an。
(II)由(I)知, an≠0,所以![]() =3, 于是数列{a2n-1}是首项a1=1,公比为3的等比数列,数列{a2n}是首项a1=2,公比为3的等比数列,所以a2n-1=3n-1, a2n=2x3n-1, 于是S2n=a1+a2+.....+a2n=(a1+a3+......a2n-1)+(a2+a4+.....+a2n)=(1+3+.....+3n-1)+2(1+3+......+3n-1)=3(1+3+......+3n-1)=
=3, 于是数列{a2n-1}是首项a1=1,公比为3的等比数列,数列{a2n}是首项a1=2,公比为3的等比数列,所以a2n-1=3n-1, a2n=2x3n-1, 于是S2n=a1+a2+.....+a2n=(a1+a3+......a2n-1)+(a2+a4+.....+a2n)=(1+3+.....+3n-1)+2(1+3+......+3n-1)=3(1+3+......+3n-1)=![]() , 从而S2n-1=S2n-a2n==
, 从而S2n-1=S2n-a2n==![]() -2x3n-1=
-2x3n-1=![]() (5x3n-2-1), 综上所述, Sn=
(5x3n-2-1), 综上所述, Sn=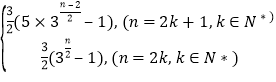
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系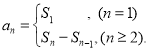 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
相关题目