题目内容
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,焦点
,焦点![]() 为
为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
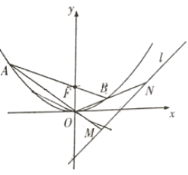
(2)过点![]() 作直线交抛物线
作直线交抛物线![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() 、
、![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由抛物线的几何性质及题设条件焦点F(0,1)可直接求得p,确定出抛物线的开口方向,写出它的标准方程;
(2)由题意,可A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1,将直线方程与(1)中所求得方程联立,再结合弦长公式用所引入的参数表示出|MN|,根据所得的形式作出判断,即可求得最小值.
(1)由已知可设抛物线的方程为:![]() ,则
,则![]() .
.
所以抛物线![]() 的方程是
的方程是![]() .
.
(2)设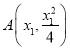 ,
,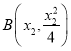 ,所以
,所以![]() ,
,![]() ,所以直线
,所以直线![]() 的方程是:
的方程是:![]() .
.
由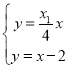 ,∴
,∴![]() ,同理由
,同理由 ,∴
,∴![]() .
.
所以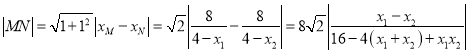 .①
.①
设![]() ,由
,由![]() ∴
∴![]() ,
,
∴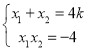
且![]() ,代入①得到:
,代入①得到:
 ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
①当![]() 时,
时,
![]() ;
;
②当![]() 时,
时,
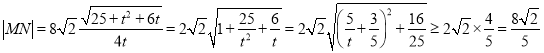 ,
,
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时,
,此时,![]() ;
;
综上所述:![]() 的最小值是
的最小值是![]() .
.

【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: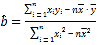 ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]()
![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
