题目内容
（2013•通州区一模）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=2，AB=2| 2 |
（Ⅰ）求证：BC⊥AM；
（Ⅱ）若N是AB上一点，且
| AN |
| AB |
| CM |
| CC1 |
（Ⅲ）若CM=
| 5 |
| 2 |
分析：（Ⅰ）证明BC⊥AM，可证BC⊥面ACM，由CC1⊥底面ABC得到BC⊥CM，在三角形ABC中由勾股定理得到AC⊥BC，由线面垂直的判定定理得到BC⊥面ACM，则问题得证；
（Ⅱ）过N作NP∥BB1交AB1于P，连结MP，由已知及三角形相似可证得四边形MCNP是平行四边形，从而得到线线平行，进一步利用线面平行的判定定理得到线面平行；
（Ⅲ）由（Ⅰ）知CA，CB，CC1为三条两两相互垂直的直线，以C为原点，CA，CB，CC1分别为x轴，y轴，z轴建立空间直角坐标系，然后利用空间向量求二面角A-MB1-C的大小．
（Ⅱ）过N作NP∥BB1交AB1于P，连结MP，由已知及三角形相似可证得四边形MCNP是平行四边形，从而得到线线平行，进一步利用线面平行的判定定理得到线面平行；
（Ⅲ）由（Ⅰ）知CA，CB，CC1为三条两两相互垂直的直线，以C为原点，CA，CB，CC1分别为x轴，y轴，z轴建立空间直角坐标系，然后利用空间向量求二面角A-MB1-C的大小．
解答：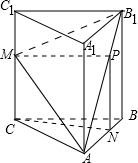
（Ⅰ）证明：因为三棱柱ABC-A1B1C1中CC1⊥平面ABC，
所以 CC1⊥BC．
因为AC=BC=2，AB=2
，
所以，由勾股定理的逆定理知BC⊥AC．
又因为AC∩CC1=C，
所以BC⊥平面ACC1A1
因为AM?平面ACC1A1，
所以BC⊥AM；
（Ⅱ）证明：如图，
过N作NP∥BB1交AB1于P，连结MP，则
NP∥CC1，且△ANP∽△ABB1．
于是有
=
．
由已知
=
，有
=
．
因为BB1=CC1．
所以NP=CM．
所以四边形MCNP是平行四边形．
所以CN∥MP．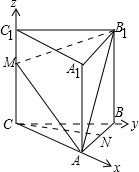
因为CN?平面AB1M，MP?平面AB1M，
所以CN∥平面AB1M；
（Ⅲ）因为BC⊥AC，且CC1⊥平面ABC，
所以以C为原点，CA，CB，CC1分别为x轴，y轴，z轴建立如图所示空间直角坐标系C-xyz．
因为CM=
，所以C（0，0，0），A（2，0，0），B1（0，2，4），M(0，0，
)，
=(-2，0，
)，
=(0，-2，-
)．
设平面AMB1的法向量
=(x，y，z)，
则
，即
，
令x=5，则y=-3，z=4，即
=(5，-3，4)．
又平面MB1C的一个法向量是
=(2，0，0)，
所以cos＜
，
＞=
=
=
．
由图可知二面角A-MB1-C为锐角，
所以二面角A-MB1-C的大小为
．
（Ⅰ）证明：因为三棱柱ABC-A1B1C1中CC1⊥平面ABC，所以 CC1⊥BC．
因为AC=BC=2，AB=2
| 2 |
所以，由勾股定理的逆定理知BC⊥AC．
又因为AC∩CC1=C，
所以BC⊥平面ACC1A1
因为AM?平面ACC1A1，
所以BC⊥AM；
（Ⅱ）证明：如图，
过N作NP∥BB1交AB1于P，连结MP，则
NP∥CC1，且△ANP∽△ABB1．
于是有
| NP |
| BB1 |
| AN |
| AB |
由已知
| AN |
| AB |
| CM |
| CC1 |
| NP |
| BB1 |
| CM |
| CC1 |
因为BB1=CC1．
所以NP=CM．
所以四边形MCNP是平行四边形．
所以CN∥MP．
因为CN?平面AB1M，MP?平面AB1M，
所以CN∥平面AB1M；
（Ⅲ）因为BC⊥AC，且CC1⊥平面ABC，
所以以C为原点，CA，CB，CC1分别为x轴，y轴，z轴建立如图所示空间直角坐标系C-xyz．
因为CM=
| 5 |
| 2 |
| 5 |
| 2 |
| AM |
| 5 |
| 2 |
| B1M |
| 3 |
| 2 |
设平面AMB1的法向量
| m |
则
|
|
令x=5，则y=-3，z=4，即
| m |
又平面MB1C的一个法向量是
| CA |
所以cos＜
| m |
| CA |
| ||||
|
|
| 5×2+(-3)×0+4×0 | ||||
|
| ||
| 2 |
由图可知二面角A-MB1-C为锐角，
所以二面角A-MB1-C的大小为
| π |
| 4 |
点评：本题考查了直线与平面平行的判定，考查了直线与平面垂直的判定，证明的关键是进口两个判定定理的条件，训练了利用平面法向量求二面角的大小，关键是会求平面的法向量，是中档题．
练习册系列答案
教材全解字词句篇系列答案
相关题目