题目内容
在⊿ABC中，BC=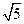
，AC=3，sinC=2sinA
(I) 求AB的值：
(II) 求sin
的值
（Ⅰ）解：在△ABC中，根据正弦定理，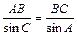
于是AB=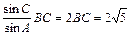
（Ⅱ）解：在△ABC中，根据余弦定理，得cosA=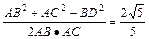
于是 sinA=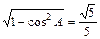
从而sin2A=2sinAcosA=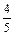
,cos2A=cos2A-sin2A=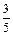
所以 sin(2A-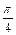
)=sin2Acos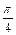-cos2Asin=
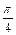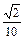
解析
练习册系列答案
相关题目
题目内容
在⊿ABC中，BC=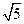，AC=3，sinC=2sinA
(I) 求AB的值：
(II) 求sin的值
（Ⅰ）解：在△ABC中，根据正弦定理，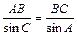
于是AB=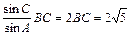
（Ⅱ）解：在△ABC中，根据余弦定理，得cosA=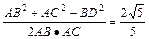
于是 sinA=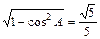
从而sin2A=2sinAcosA=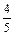,cos2A=cos2A-sin2A=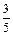
所以 sin(2A-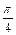)=sin2Acos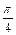-cos2Asin=
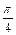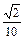
解析
北偏东
方向的点
处有一观测站，港口正东方向的
处有一轮船，测得
为
海里. 该轮船从
海里后到达
处，测得
为
海里. 问此时轮船离港口
中，
是
的中点，
是
的中点，
的延长线交
于
.
的值；
的面积为
，四边形
的面积为
，求
的值．
中，角A、B、C的对边分别为a、b、c，已知
，
，求b边的长。
（
），且函数
的最小正周期为
.
中，角
所对的边分别为
．若
，
，且
，试求
的值.
中，角A、B、C所对边分别是a、b、c，
，求
．
中，角
所列边分别为
，且
；
，试判断
取得最大值时
，
，其中０＜
＜
．
=
，求角
的面积为
，求
的值
.
的长；
是
的中点，求中线
的长度.