题目内容
【题目】已知![]() 是二次函数,其函数图像经过(0,2),
是二次函数,其函数图像经过(0,2),![]() 在
在![]() 时取得最小值1.
时取得最小值1.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在[k,k+1]上的最小值.
在[k,k+1]上的最小值.
【答案】(1)f(x)=(x-1)2+1.
(2)g(k)=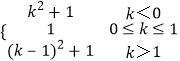
【解析】
(1)根据f(x+1)在x=0时取得最小值1可设f(x+1)=ax2+1,从而得到f(x)=a(x﹣1)2+1,根据f(x)的图象过点(0,2)可求出a=1,从而得出f(x)解析式;
(2)f(x)的对称轴为x=1,讨论区间[k,k+1]的端点和对称轴的关系:k+1<1,k≤1≤k+1,k>1,根据二次函数的单调性及顶点情况便可求出每种情况的f(x)在[k,k+1]上的最小值.
(1)设f(x)=a(x-1)2+1;
由f(0)=a+1=2得a=1;
∴f(x)=(x-1)2+1;
(2)①当k+1<1,即k<0时,最小值g(k)=f(k+1)=k2+1;
②当k>1时,最小值g(k)=f(k)=(k-1)2+1;
③当0≤k≤1时,最小值g(k)=f(1)=1;
综上g(k)=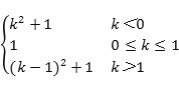 .
.

练习册系列答案
相关题目


