题目内容
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.(Ⅰ)试确定A1P:PB的值,使得PC⊥AB;
(Ⅱ)若A1P:PB=2:3,求二面角P-AC-B的大小.
分析:【法一】(Ⅰ)利用三角形的中位线,可确定A1P:PB的值,使得PC⊥AB;
(Ⅱ)先作出二面角P-AC-B的平面角,再进行计算;
【法二】建立空间直角坐标系,(Ⅰ)由
•
=0,可确定A1P:PB的值,使得PC⊥AB;
(Ⅱ)确定平面的法向量,利用向量的夹角公式,即可求得结论.
(Ⅱ)先作出二面角P-AC-B的平面角,再进行计算;
【法二】建立空间直角坐标系,(Ⅰ)由
| CP |
| AB |
(Ⅱ)确定平面的法向量,利用向量的夹角公式,即可求得结论.
解答:解:【法一】(Ⅰ)当PC⊥AB时,作P在AB上的射影D,连接CD,则AB⊥平面PCD,∴AB⊥CD,∴D是AB的中点,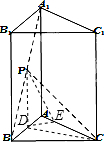
又PD∥AA1,∴P也是A1B的中点,即A1P:PB=1.
反之当A1P:PB=1时,取AB的中点D',连接CD'、PD'.
∵△ABC为正三角形,∴CD'⊥AB.
由于P为A1B的中点时,PD'∥A1A
∵A1A⊥平面ABC,∴PD'⊥平面ABC,∴PC⊥AB.…6′
(Ⅱ)当A1P:PB=2:3时,作P在AB上的射影D,则PD⊥底面ABC.
作D在AC上的射影E,连接PE,则PE⊥AC,∴∠DEP为二面角P-AC-B的平面角.
又∵PD∥AA1,∴
=
=
,∴AD=
a.
∴DE=AD•sin60°=
a,
又∵
=
,∴PD=
a,∴tan∠PED=
=
,∴P-AC-B的大小为∠PED=60°.…12
【法二】以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA1为z轴,建立空间直角坐标系A-xyz,如图所示,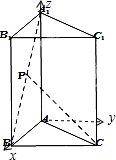 设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(
设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(
,
,0).
(Ⅰ)由
•
=0得(x-
,-
,z)•(a,0,0)=0,即(x-
)•a=0,
∴x=
a,即P为A1B的中点,也即A1P:PB=1时,PC⊥AB.…4′
(Ⅱ)当A1P:PB=2:3时,P点的坐标是(
,0,
).
取
=(3,-
,-2).则
•
=(3,-
,-2)•(
,0,
)=0,
•
=(3,-
,-2)•(
,
,0)=0.
∴
是平面PAC的一个法向量.
又平面ABC的一个法向量为
=(0,0,1).
∴cos<
,
>=
=
,∴二面角P-AC-B的大小是60°.…(12分)

又PD∥AA1,∴P也是A1B的中点,即A1P:PB=1.
反之当A1P:PB=1时,取AB的中点D',连接CD'、PD'.
∵△ABC为正三角形,∴CD'⊥AB.
由于P为A1B的中点时,PD'∥A1A
∵A1A⊥平面ABC,∴PD'⊥平面ABC,∴PC⊥AB.…6′
(Ⅱ)当A1P:PB=2:3时,作P在AB上的射影D,则PD⊥底面ABC.
作D在AC上的射影E,连接PE,则PE⊥AC,∴∠DEP为二面角P-AC-B的平面角.
又∵PD∥AA1,∴
| BD |
| DA |
| BP |
| PA1 |
| 3 |
| 2 |
| 2 |
| 5 |
∴DE=AD•sin60°=
| ||
| 5 |
又∵
| PD |
| AA1 |
| 3 |
| 5 |
| 3 |
| 5 |
| PD |
| DE |
| 3 |
【法二】以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA1为z轴,建立空间直角坐标系A-xyz,如图所示,
 设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(
设P(x,0,z),则B(a,0,0)、A1(0,0,a)、C(| a |
| 2 |
| ||
| 2 |
(Ⅰ)由
| CP |
| AB |
| a |
| 2 |
| ||
| 2 |
| a |
| 2 |
∴x=
| 1 |
| 2 |
(Ⅱ)当A1P:PB=2:3时,P点的坐标是(
| 2a |
| 5 |
| 3a |
| 5 |
取
| m |
| 3 |
| m |
| AP |
| 3 |
| 2a |
| 5 |
| 3a |
| 5 |
| m |
| AC |
| 3 |
| a |
| 2 |
| ||
| 2 |
∴
| m |
又平面ABC的一个法向量为
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 1 |
| 2 |
点评:本题考查线线垂直,考查面面角,考查利用向量知识解决立体几何问题,确定平面的法向量是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为