题目内容
如图，已知正三棱柱ABC-A1B1C1，D是AC的中点，∠C1DC=600，则异面直线AB1与C1D所成角的余弦值为（ ）分析：连接B1C，取B1C中点E，连接C1E、DE．设AD=DC=1，则Rt△C1DC中利用60°角的三角函数，可算出CC1=
，C1D=2，再用勾股定理算出AB1=B1C=
，从而得出在△C1DE中，DE=C1E=
，由余弦定理得cos∠C1DE=
，最后由异面直线所成角的定义得到异面直线AB1与C1D所成角的余弦值．
| 3 |
| 7 |
| ||
| 2 |
2
| ||
| 7 |
解答：解：连接B1C，取B1C中点E，连接C1E、DE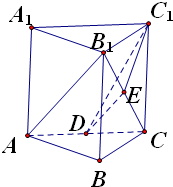
设AD=DC=1，则Rt△C1DC中，tan∠C1DC=
=
∴CC1=
CD=
，C1D=2
矩形BCC1B1中，B1C=
=
，可得C1E=
又∵△AB1C中，AB1=B1C=
，DE是中位线
∴DE=
AB1=
因此，在△C1DE中，由余弦定理得：cos∠C1DE=
=
∵DE∥AB1，
∴锐角∠C1DE就是直线AB1与C1D所成的角，可得异面直线AB1与C1D与所成角的余弦值为
故选B
设AD=DC=1，则Rt△C1DC中，tan∠C1DC=
| CC1 |
| CD |
| 3 |
∴CC1=
| 3 |
| 3 |
矩形BCC1B1中，B1C=
| BC2+CC22 |
| 7 |
| ||
| 2 |
又∵△AB1C中，AB1=B1C=
| 7 |
∴DE=
| 1 |
| 2 |
| ||
| 2 |
因此，在△C1DE中，由余弦定理得：cos∠C1DE=
| DE2+C1D2-C1E2 |
| 2DE•C1D |
2
| ||
| 7 |
∵DE∥AB1，
∴锐角∠C1DE就是直线AB1与C1D所成的角，可得异面直线AB1与C1D与所成角的余弦值为
2
| ||
| 7 |
故选B
点评：本题在正三棱柱中求异面直线所成的角，着重考查了正棱柱的性质、异面直线所成的定义和余弦定理等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为线段A1B上的动点．
如图，已知正三棱柱ABC-A1B1C1的底面边长为2cm，高位5cm，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图，已知正三棱柱ABC-A1B1C1的各条棱长都为a，P为A1B上的点．
（2011•重庆三模）如图，已知正三棱柱ABC-A1B1C1的所有棱长均为a，截面AB1C和A1BC1相交于DE，则三棱锥B-B1DE的体积为