题目内容
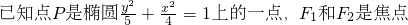 ,且∠F1PF2=30°,求△F1PF2的面积.
,且∠F1PF2=30°,求△F1PF2的面积.
解: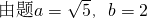 ,∴
,∴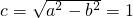 又∵P在椭圆上,∴
又∵P在椭圆上,∴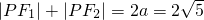 由余弦定理得:|PF1|2+|PF2|2-2|PF1|•|PF2|•cos30°=|F1F2|2=(2c)2=4
由余弦定理得:|PF1|2+|PF2|2-2|PF1|•|PF2|•cos30°=|F1F2|2=(2c)2=4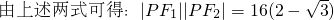 ∴
∴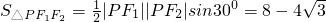 .
.
分析:首先由椭圆方程求出a、b、c的值,然后根据椭圆的定义得出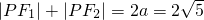 ,再由余弦定理,可以求得|PF1|•|PF2|,从而求出三角形的面积.
,再由余弦定理,可以求得|PF1|•|PF2|,从而求出三角形的面积.
点评:本题考查了椭圆的性质,余弦定理的运用,对于求三角形的面积要根据条件选择面积公式.属于中档题.
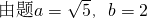 ,∴
,∴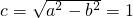 又∵P在椭圆上,∴
又∵P在椭圆上,∴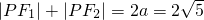 由余弦定理得:|PF1|2+|PF2|2-2|PF1|•|PF2|•cos30°=|F1F2|2=(2c)2=4
由余弦定理得:|PF1|2+|PF2|2-2|PF1|•|PF2|•cos30°=|F1F2|2=(2c)2=4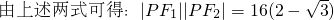 ∴
∴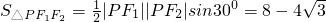 .
.分析:首先由椭圆方程求出a、b、c的值,然后根据椭圆的定义得出
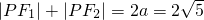 ,再由余弦定理,可以求得|PF1|•|PF2|,从而求出三角形的面积.
,再由余弦定理,可以求得|PF1|•|PF2|,从而求出三角形的面积.点评:本题考查了椭圆的性质,余弦定理的运用,对于求三角形的面积要根据条件选择面积公式.属于中档题.

练习册系列答案
相关题目