题目内容
14.x∈R,用记号N(x)表示不小于实数的最小整数,例如N(2.5)=3,$N({-\sqrt{2}})=-1$,N(1)=1;则函数$f(x)=N({3x+1})-2x+\frac{1}{2}$的所有零点之和为-4.分析 作函数y=3x+1与函数y=2x-$\frac{1}{2}$的图象,结合图象讨论以确定方程N(3x+1)=2x-$\frac{1}{2}$的解,从而求函数$f(x)=N({3x+1})-2x+\frac{1}{2}$的所有零点之和.
解答 解:作函数y=3x+1与函数y=2x-$\frac{1}{2}$的图象如下,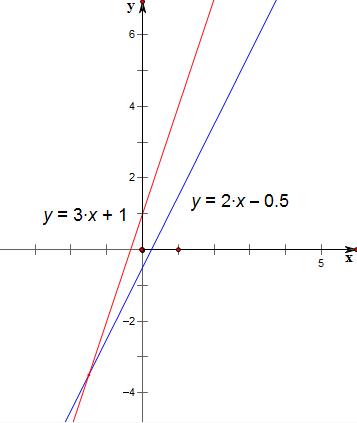
①当-4<3x+1≤-3时,N(3x+1)=-3,故2x-$\frac{1}{2}$=-3,
解得,x=-$\frac{5}{4}$(舍去);
②当-5<3x+1≤-4时,N(3x+1)=-4,故2x-$\frac{1}{2}$=-4,
解得,x=-$\frac{7}{4}$;
③当-6<3x+1≤-5时,N(3x+1)=-5,故2x-$\frac{1}{2}$=-5,
解得,x=-$\frac{9}{4}$;
④当-7<3x+1≤-6时,N(3x+1)=-6,故2x-$\frac{1}{2}$=-6,
解得,x=-$\frac{11}{4}$(舍去);
故函数$f(x)=N({3x+1})-2x+\frac{1}{2}$的所有零点之和为
-$\frac{7}{4}$-$\frac{9}{4}$=-4;
故答案为:-4.
点评 本题考查了数形结合的应用及分类讨论的思想应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.某几何体的三视图(单位:cm)如图,则这个几何体的体积为( )cm3.


| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $6\sqrt{3}$ |
3.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,记椭圆与双曲线的离心率分别为e1,e2,则e1•e2的取值范围是( )
| A. | ($\frac{1}{3}$,+∞) | B. | ($\frac{1}{5}$,+∞) | C. | ($\frac{1}{9}$,+∞) | D. | (0,+∞) |
 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图(2)所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图(2)所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q. 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;