题目内容
下列命题:
(1)若向量|
|=|
|,则
与
的长度相等且方向相同或相反;
(2)对于任意非零向量若|
|=|
|且
与
的方向相同,则
=
;
(3)非零向量
与非零向量
满足
∥
,则向量
与
方向相同或相反;
(4)向量
与
是共线向量,则A,B,C,D四点共线;
(5)若
∥
,且
∥
,则
∥
正确的个数( )
(1)若向量|
| a |
| b |
| a |
| b |
(2)对于任意非零向量若|
| a |
| b |
| a |
| b |
| a |
| b |
(3)非零向量
| a |
| b |
| a |
| b |
| a |
| b |
(4)向量
| AB |
| CD |
(5)若
| a |
| b |
| b |
| c |
| a |
| c |
正确的个数( )
分析:(1)根据模相等的定义即可判断出;
(2)根据相等向量的定义即可得出;
(3)根据共线向量的定义即可判断出;
(4)根据共线向量的定义即可判断出;
(5)当
=
时,不一定有
∥
.
(2)根据相等向量的定义即可得出;
(3)根据共线向量的定义即可判断出;
(4)根据共线向量的定义即可判断出;
(5)当
| b |
| 0 |
| a |
| c |
解答:解:(1)若向量|
|=|
|,则
与
的长度相等而方向可以任意,故不正确;
(2)根据相等向量的定义可知:正确;
(3)根据共线向量的定义可知:正确;
(4)向量
与
是共线向量,则A,B,C,D四点共线或AB∥CD,故不正确;
(5)若
=
,则
与
不一定共线,故不正确.
综上可知:只有(2)(3)正确.
故选C.
| a |
| b |
| a |
| b |
(2)根据相等向量的定义可知:正确;
(3)根据共线向量的定义可知:正确;
(4)向量
| AB |
| CD |
(5)若
| b |
| 0 |
| a |
| c |
综上可知:只有(2)(3)正确.
故选C.
点评:正确理解模相等的定义、相等向量的定义、共线向量的定义是解题额根据.

练习册系列答案
相关题目
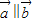 ,
,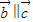 ,则
,则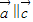 ;
;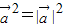 .
.