题目内容
已知函数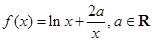 .
.
(1)若函数 在
在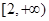 上是增函数,求实数
上是增函数,求实数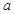 的取值范围;
的取值范围;
(2)若函数 在
在 上的最小值为3,求实数
上的最小值为3,求实数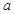 的值.
的值.
(1)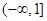 ;(2)
;(2)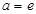 .
.
解析试题分析:(1)这是一个由函数在某区间上是增函数,求参数取值范围的问题,可转化为其导函数在此区间上恒大于或等于0的一个恒成立问题,恒成立问题是我们所熟悉的问题,可分离参数解答,也可由函数本身的性质作出判断;(2)这是一个求含参函数在某区间上的最小值问题,可通过导数的符号去判断函数的单调区间,当然一般会涉及对参数的讨论,之后利用单调性则可求出函数的最小值,再由最小值为3,就可求出参数的值.
试题解析:(1)∵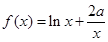 ,∴
,∴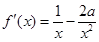 .
.
∵ 在
在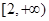 上是增函数,
上是增函数,
∴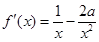 ≥0在
≥0在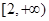 上恒成立,即
上恒成立,即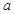 ≤
≤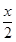 在
在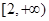 上恒成立.
上恒成立.
令 ,则
,则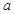 ≤
≤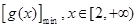 .
.
∵ 在
在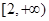 上是增函数,∴
上是增函数,∴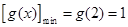 .
.
∴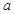 ≤1.所以实数
≤1.所以实数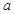 的取值范围为
的取值范围为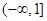 .
.
(2)由(1)得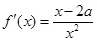 ,
, .
.
①若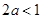 ,则
,则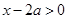 ,即
,即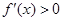 在
在 上恒成立,此时
上恒成立,此时 在
在 上是增函数.
上是增函数.
所以 ,解得
,解得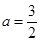 (舍去).
(舍去).
②若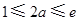 ,令
,令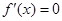 ,得
,得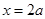 .当
.当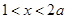 时,
时,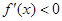 ,所以
,所以 在
在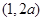 上是减函数,当
上是减函数,当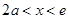 时,
时,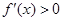 ,所以
,所以 在
在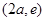 上是增函数.
上是增函数.
所以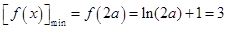 ,解得
,解得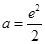 (舍去).
(舍去).
③若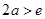 ,则
,则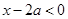 ,即
,即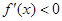 在
在 上恒成立,此时
上恒成立,此时 在
在 上是减函数.
上是减函数.
所以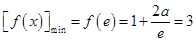 ,所以
,所以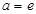 .
.
考点:函数与导数、函数的单调性.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
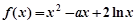 (其中
(其中 是实数).
是实数).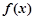 的单调区间;
的单调区间; ,且
,且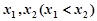 ,求
,求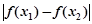 的取值范围.
的取值范围.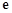 是自然对数的底数)
是自然对数的底数)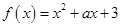 .
.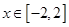 时,
时,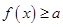 恒成立,求实数
恒成立,求实数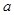 的取值范围;
的取值范围;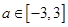 ,
,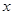 的取值范围.
的取值范围.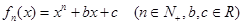
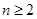 ,
,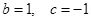 ,证明:
,证明: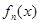 在区间
在区间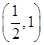 内存在唯一的零点;
内存在唯一的零点;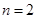 ,若对任意
,若对任意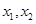
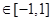 ,有
,有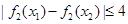 ,求
,求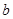 的取值范围
的取值范围 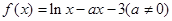
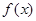 的单调性;
的单调性;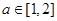 ,若函数
,若函数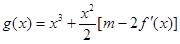 在 区间
在 区间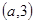 上有最值,求实数
上有最值,求实数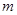 的取值范围.
的取值范围.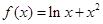 .
.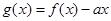 在定义域内为增函数,求实数
在定义域内为增函数,求实数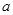 的取值范围;
的取值范围;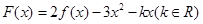 ,若函数
,若函数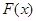 存在两个零点
存在两个零点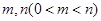 ,且实数
,且实数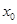 满足
满足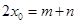 ,问:函数
,问:函数 处的切线能否平行于
处的切线能否平行于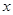 轴?若能,求出该切线方程;若不能,请说明理由.
轴?若能,求出该切线方程;若不能,请说明理由. 。
。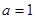 ,求函数
,求函数 的单调递减区间;
的单调递减区间;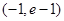 上单调递增,求实数
上单调递增,求实数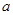 的取值范围;
的取值范围;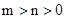 时,
时,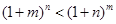
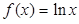 .
.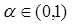 ,求
,求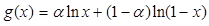 最大值;
最大值;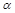 ,
,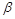 满足
满足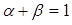 .求证:
.求证: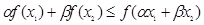 ;
;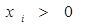 ,正数
,正数 满足
满足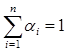 .证明:
.证明: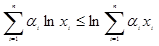
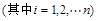 .
.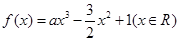 ,其中
,其中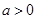 .
. ,求曲线
,求曲线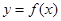 在点
在点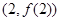 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围.