Question

将函数y=

4+6x-x2

-2（x∈[0，6]）的图象绕坐标原点逆时针方向旋转角θ（0≤θ≤α），得到曲线C．若对于每一个旋转角θ，曲线C都是一个函数的图象，则α的最大值为

 

．

Answer 1

分析：先画出函数y=

4+6x-x2

-2（x∈[0，6]）的图象，然后根据由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时，曲线C都不是一个函数的图象，求出此角即可．

解答：解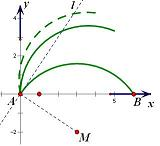：先画出函数y=

4+6x-x2

-2（x∈[0，6]）的图象
这是一个圆弧，圆心为M（3，-2）
由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时，
曲线C都不是一个函数的图象
∴∠MAB=arctan

2

3

故答案为：arctan

2

3

点评：本题主要考查了旋转变换，同时考查了数形结合的思想和分析问题解决问题的能力，属于基础题．