题目内容
6．设P（1，f（1））是曲线C：f（x）=x2+2x+3上的一点，则曲线C过点P的切线方程是（ ）| A． | 4x-y+10=0 | B． | 4x-y+2=0 | C． | x-4y+10=0 | D． | x-4y+2=0 |
分析 由题意可得曲线C过点P的切线以点P为切点，从而利用导数求切线的斜率，从而解得．
解答 解：∵f（x）=x2+2x+3是二次函数，且P（1，f（1））是其图象上的一点，
∴曲线C过点P的切线以点P为切点；
又∵f′（x）=2x+2，
∴切线的斜率k=f′（1）=2+2=4，
又∵f（1）=1+2+3=6；
故切线方程为y-6=4（x-1），
即4x-y+2=0；
故选：B．
点评 本题考查了导数的几何意义的应用及二次函数的性质应用，属于中档题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
17．四条曲线x2=2y，x=2，x=-2，y=0围成的封闭图形绕y轴旋转一周所得的旋转体的体积为V1：满足$\left\{\begin{array}{l}y≥0\\{x^2}+{（{y-1}）^2}≤1\\{x^2}+{y^2}≤4\end{array}\right.$的平面区域绕y轴旋转一周所得的旋转体的体积为V2，则（ ）
| A． | V1＞V2 | B． | V1＜V2 | ||
| C． | V1=V2 | D． | V1，V2无明确大小关系 |
14．已知实数x、y满足$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x-y≥0}\end{array}\right.$ 则z=$\frac{y-1}{x}$的取值范围是（ ）
| A． | [-1，0] | B． | [-1，1） | C． | （-∞，0] | D． | [-1，+∞） |
15．双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1与双曲线$\frac{x^2}{16-t}-\frac{y^2}{t+9}$=1（-9＜t＜16 ）的（ ）
| A． | 实轴长相等 | B． | 虚轴长相等 | C． | 焦距相等 | D． | 离心率相等 |
16．
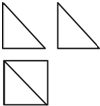利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）
利用一球体毛坯切削后得到一个几何体，该几何体的三视图如图所示，若主视图和左视图都是直角边长为1的等腰直角三角形，则毛坯球体的体积最小应为（ ）| A． | $\frac{{\sqrt{2}π}}{3}$ | B． | $\frac{4π}{3}$ | C． | $\frac{\sqrt{3}π}{2}$ | D． | $\frac{8\sqrt{2}π}{3}$ |