题目内容
已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4).设a=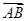 ,b=
,b=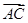 .
.
(1)求a和b的夹角θ;
(2)若向量ka+b与ka-2b互相垂直,求k的值.
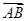 ,b=
,b=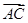 .
.(1)求a和b的夹角θ;
(2)若向量ka+b与ka-2b互相垂直,求k的值.
(1)arccos (2)k=-
(2)k=-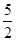 或2.
或2.
 (2)k=-
(2)k=-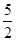 或2.
或2.∵A(-2,0,2),B(-1,1,2),C(-3,0,4),a=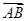 ,b=
,b=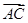 ,
,
∴a=(1,1,0),b=(-1,0,2).
(1)∵cosθ=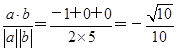 ,∴a和b的夹角为arccos
,∴a和b的夹角为arccos .
.
(2)∵ka+b=k(1,1,0)+(-1,0,2)=(k-1,k,2),
ka-2b=(k+2,k,-4),且(ka+b)⊥(ka-2b),
∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8
=2k2+k-10=0,解得k=-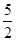 或2.
或2.
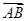 ,b=
,b=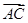 ,
,∴a=(1,1,0),b=(-1,0,2).
(1)∵cosθ=
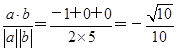 ,∴a和b的夹角为arccos
,∴a和b的夹角为arccos .
.(2)∵ka+b=k(1,1,0)+(-1,0,2)=(k-1,k,2),
ka-2b=(k+2,k,-4),且(ka+b)⊥(ka-2b),
∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8
=2k2+k-10=0,解得k=-
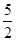 或2.
或2.
练习册系列答案
相关题目
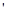 D,使得平面BC
D,使得平面BC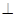 平面ABD.
平面ABD.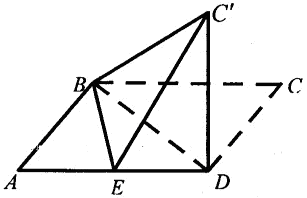
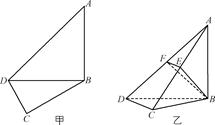
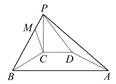
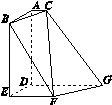
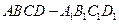 中,点E为
中,点E为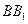 的中点,则平面
的中点,则平面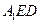 与平面ABCD所成的锐二面角的余弦值为( )
与平面ABCD所成的锐二面角的余弦值为( )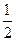
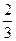
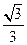
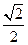
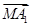 +
+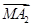 +
+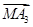 +
+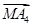 +
+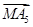 =0成立的点M的个数为________.
=0成立的点M的个数为________.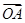 =a,
=a,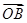 =b,
=b,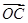 =c,用a,b,c表示向量
=c,用a,b,c表示向量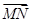 =________.
=________.
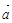 =(2,4,x),
=(2,4,x),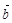 =(2,y,2),若|
=(2,y,2),若|