题目内容
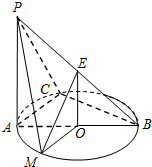 如图所示,AB是⊙O的直径,点C是⊙O圆周上不同于A、B的任意一点,PA⊥平面ABC,点E是线段PB的中点,点M在
如图所示,AB是⊙O的直径,点C是⊙O圆周上不同于A、B的任意一点,PA⊥平面ABC,点E是线段PB的中点,点M在 | AB |
(1)求证:BC⊥平面PAC;
(2)求证:平面EOM∥平面PAC.
分析:(1)由PA⊥平面ABC,证出PA⊥BC,由直径所对的圆周角证出BC⊥AC,再利用线面垂直判定定理,即可证出BC⊥平面PAC.
(2)根据三角形中位线定理证出EO∥PA,从而得到EO∥平面PAC,由MO∥AC证出MO∥平面PAC,再结合面面平行判定定理即可证出平面EOM∥平面PAC.
(2)根据三角形中位线定理证出EO∥PA,从而得到EO∥平面PAC,由MO∥AC证出MO∥平面PAC,再结合面面平行判定定理即可证出平面EOM∥平面PAC.
解答:解:(1)∵点C是以AB为直径的⊙O圆周上不同于A、B的任意一点,
∴∠ACB=90°,即BC⊥AC.
∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵AC?平面PAC,PA?平面PAC,AC∩PA=A,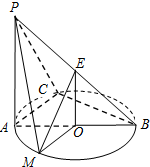
∴BC⊥平面PAC.
(2)∵点E是线段PB的中点,点O是线段AB的中点,
∴EO∥PA.
∵PA?平面PAC,EO?平面PAC,∴EO∥平面PAC.
∵MO∥AC,AC?平面PAC,MO?平面PAC,
∴MO∥平面PAC.
∵EO?平面EOM,MO?平面EOM,EO∩MO=O,
∴平面EOM∥平面PAC.
∴∠ACB=90°,即BC⊥AC.
∵PA⊥平面ABC,BC?平面ABC,
∴PA⊥BC.
∵AC?平面PAC,PA?平面PAC,AC∩PA=A,

∴BC⊥平面PAC.
(2)∵点E是线段PB的中点,点O是线段AB的中点,
∴EO∥PA.
∵PA?平面PAC,EO?平面PAC,∴EO∥平面PAC.
∵MO∥AC,AC?平面PAC,MO?平面PAC,
∴MO∥平面PAC.
∵EO?平面EOM,MO?平面EOM,EO∩MO=O,
∴平面EOM∥平面PAC.
点评:本题给出特殊锥体,求证线面垂直并证明面面平行,着重考查直线与平面垂直的判定、平面与平面平行的判定定理等知识,考查空间想象能力,属于中档题.

练习册系列答案
相关题目
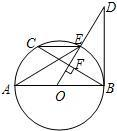 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB.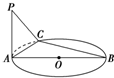 如图所示,AB是⊙O的直径,PA⊥平面⊙O,C为圆周上一点,AB=5cm,AC=2cm,则B到平面PAC的距离为
如图所示,AB是⊙O的直径,PA⊥平面⊙O,C为圆周上一点,AB=5cm,AC=2cm,则B到平面PAC的距离为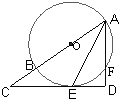 (2013•东莞二模)(几何证明选讲选做题)
(2013•东莞二模)(几何证明选讲选做题)